Уравнение бегущей волны. Фазовая скорость. Волновое уравнение

Рассмотрим плоскую синусоидальную волну, предполагая, что ось х совпадает е направлением распространения волны (см. рис. 4.1).

В данной случае волновое поверхности перпендикулярны. оси х, а так как все точки волновом поверхности колеблются одинаково, то смещение будет зависеть только от х и t т.е. .

На рис. 4.1 рассмотрим некоторую частицу В, находящуюся от источника колебаний 0 на расстоянии х. Если колебания точек, лежащих в плоскости х =0, описывается функцией , то точка среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на , так как для прохождения волной расстояния х требуется время

где - скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид:

(4.2)

Откуда следует важный признак волны: волна - это процесс, периодический во времени и пространстве. Уравнение (4.2) есть уравнение бегущей волны. Если плоская волна распространяется в противоположим направлении, то

В общем случае уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергии, имеет вид:

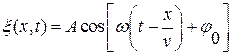(4.3)

где А =const – амплитуда волны,

– циклическая частота волна,

– начальная фаза колебаний, определяемая в общем случае выбором начала отсчета х и t, – фаза плоской волны.

Для характеристики синусоидальной волны используется волновое число:

(4.4)

Учитывая формулу (4.4), уравнению (4.3) можно придать вид:

(4.5)

Уравнение волны, распространяющейся в сторону убывания X, отличается от уравнения (4.5) только знаком члена kx

Предположим, что при волновом процессе фаза постоянна, т.е.

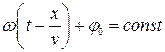(4.6)

Продифференцировав выражение (4.6), получим:

откуда,

(4.7)

Следовательно, скорость v распространения волны в уравнении (4.7) есть не что иное, как скорость перемещения фазы волны, и называется её фазовой скоростью.

Уравнение сферической синусоидальной волны – волны, волновые поверхности которой имеет вид концентрических сфер, записывается как

(4.8)

где r – расстояние от центра волны до рассматриваемой точки среды.

В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону . Уравнение (4.8) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебания можно считать точечным).

Из выражения (4.4) вытекает, что

(4.9)

т.е. фазовая скорость синусоидальных волн зависит от их частоты. Это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением: