Принцип суперпозиции. Групповая скорость

Если среда, в которой распространяется одновременно несколько, волн, линейна, т.е. ее свойства не изменяется под воздействий, возмущений, создаваемых волной, то к ним применяется принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумке смещений, которые получают частицы, участвуя в каждом из слагаемых волновых процессов. Любая волна может быть представлена в виде системы синусоидальных волн, т.е. в виде волнового пакета или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

Рассмотрим простейший волновой пакет из двух распространяющихся вдоль оси х волн с одинаковыми амплитудами и близкими частотами и волновыми числами, причем d ω << ω и d k << k.

Тогда

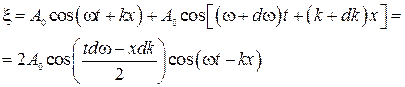
Эта волна отличается от синусоидальной тем, что ее амплитуда

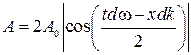есть медленно изменяющаяся функция координаты X от времени t.

В качестве скорости распространения волнового пакета принимает скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что

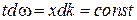, получим:

(4.12)

Скорость u - групповая скорость, скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет.

Учитывая, что 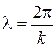найдем связь групповой u и фазовой 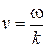скоростью.

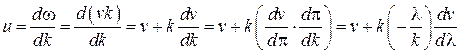
или

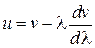(4.13)

Из формулы (4.13) следует, что u может быть как меньше, так и больше v в зависимости от знака 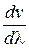. В недиспергирующей среде 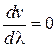и групповая скорость совпадает с фазовой.

Групповая скорость – скорость 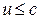(скорость света), для фазовой скорости ограничений не существует.

Интерференция волн

Волны называются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентным» могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазана этих волн. Это явление называется интерференцией волн.

Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S ₁ и S ₂, смотри рис. 4.2, колеблющимися с одинаковыми амплитудами А₀ и частотой ω и постоянной разностью фаз.

Согласно уравнению (4.8) где ,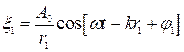

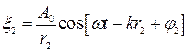
r ₁, r ₂ – расстояние от источников волн до рассматриваемой точки В, k – волновое число;

φ ₁, φ ₂ – начальные фазы.

Можно показать, что амплитуда результирующей волны в точке В равна:

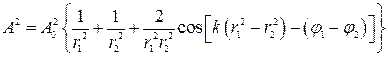Так как для когерентных источников разность начальных фаз , то результат интерференции двух волн в различных точках зависит от величины 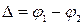, называемой разностью фаз волн. В точках, где

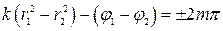(m =0,1,2,…) (4.14)

Наблюдается интерференционный максимум.

Амплитуда результирующего колебания 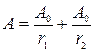. В точках, где

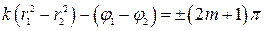(m =0,1,2,…) (4.15)

наблюдается интерференционный минимум.

Амплитуда результирующего колебания .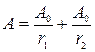

Число m =0,1,2,…называется соответственно порядком интерференционного максимума или минимума. На рис. 4.2 сплошные линии – геометрическое место точек, где образуется максимум, пунктирные – минимум.

Стоячие волны

Стоячие волны - волны, образующиеся при наложении двух бегущих синусоидальных волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Предположим, что волны распространяются навстречу друг другу без затухания, причем в начале координат фазы зоны совпадают, тогда

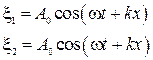(4.16)

Складывая 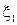и 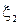учитывая, что 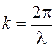получаем уравнение стоячей волны:

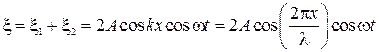(4.17)

Из уравнения стоячей волны (4.17) вытекает, что в каждой точке стоячей волны происходят колебания той же частоты ω с амплитудой 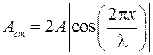зависящей от координаты х в рассматриваемой точке.

В точках среды, где

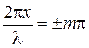
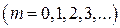(4.18)

амплитуда стоячей волны достигает максимального значения, равного 2 А.

В точках среды, где

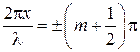
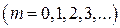(4.19)

амплитуда стоячей волны обращается в нуль. Точки, в которых амплитуда стоячей волны максимальна, называется пучностями стоячей волны, а точки, в которых амплитуда равна нулю – узлами стоячей волны.

Из выражений (4.18) к (4.19) получаем соответственно координаты пучностей узлов:

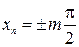
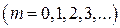4.20)

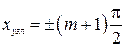
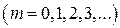(4.21)

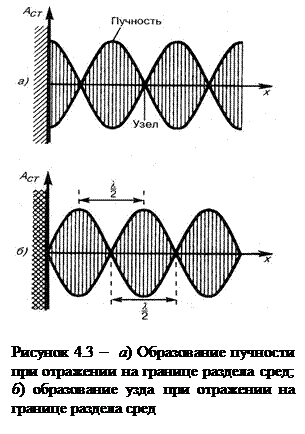
В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе (4.16) бегущей волны, фаза колебаний зависит от координаты х рассматриваемой точки). Все точки стоячей волны между двумя узлами колеблются с разными амплитудами, но с одинаковыми фазами (4.17) стоячей волны аргумент косинуса не зависит от х, При переходе через узел множитель 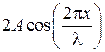меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на π т.е. точки, лежащие по разные, стороны от узла, колеблется в противофазе. Образование стоячих волн наблюдает обычно при интерференции бегущей и отраженной волн. На границе, где происходит отражение волны получается пучность или узел. Если среда, от которой происходит отражение менее плотная, то в месте отражения получается пучность (рис. 4.3, а), если среда более плотная – узел (рис. 4.3б).

ТЕОРИЯ МЕТОДА

Колебания струны приближается по характеру к поперечный волнам для которых скорость.

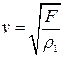(4.22)

где F – сила натяжения струны;

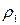– линейная плотность.

Колебания струны будут устойчивыми, если ее длина l с длиной бегущей волны λ будет связана соотношением:

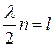(4.23)

где n – целое число (число стоячих волн).

Из уравнений (4.22), (4.23) и (4.1) получаем:

(4.24)

Сила натяжения струны может быть выражена через массу груза, натягивав него струну F = mg. Линейную плотность струны 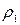найдем через плотность струны 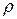, ее длину и диаметр поперечного сечения d