Понятие производной
Определение. Производной функции  в точке
в точке  называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при  (при условии, что этот предел существует).
(при условии, что этот предел существует).
Производная обозначается  или
или 
Итак, по определению,  .
.
Нахождение производной называется дифференцированием функции.
Исходя из определения, составить, опираясь на рассуждения студентов, алгоритм отыскания производной.

Пусть функция у = f (x) определена в точке х0 и во всех точках, достаточно близких в точке х0, т.е. в некоторой окрестности точки х0. тогда выберем приращение аргумента ∆х такое, что х0 + ∆х не выходит за пределы этой окрестности. Тогда составим и вычислим предел отношения приращения функции к приращению аргумента при условии ∆х→ 0. Если этот предел имеет конечное значение, то он называется производной функции f (x) в точке х0 , т.е. 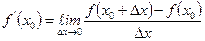
Для производной используются также другие обозначения: 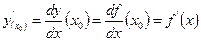
Теорема: если функция у = f (x) имеет производную в точке х0 , то она непрерывна в этой точке (обратное утверждение в общем случае неверно).
Геометрический смысл производной функции f (x) в точке х0 состоит в том. Что она равна тангенсу угла наклона (т.е. угловому коэффициенту) касательной, проведенной в этой же точке.
Понятие производной впервые ввели: Ньютон, исходя из задач механики, и Лейбниц, исходя из геометрических построений, которые мы только что рассмотрели.
Уравнение касательной.
Касательная проходит через точку с координатами (х0; f(х0)) и имеет угловой коэффициент  , тогда получим следующее уравнение касательной:
, тогда получим следующее уравнение касательной:

Уравнение нормали к кривой.
Нормалью к кривой будем называть прямую линию, проходящую через точку касания перпендикулярно касательной (смотри рис.1).
Нормаль проходит через ту же самую точку с координатами (х0; f(х0)), угловой коэффициент нормали:  . Получим уравнение:
. Получим уравнение: 
Геометрический смысл производной.
Обозначим угол наклона секущей через β. Тогда:  .
.
Устремим ∆х к нулю, тогда секущая превратиться в касательную, проведенную к кривой в точке х0. угол наклона касательной обозначим через a.
Получим: 
 |  |
∆х→ 0
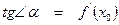
Пример1. Используя определение производной, найти производную функции 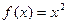 в точке
в точке  . Решение. Придавая аргументу
. Решение. Придавая аргументу  в точке
в точке  приращения
приращения 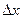 , найдем соответствующее приращение функции:
, найдем соответствующее приращение функции: 
Составим соотношение  .Найдем предел этого отношения при
.Найдем предел этого отношения при

Следовательно, производная функции 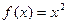 в точке
в точке  равна числу 2
равна числу 2  , что в принятых обозначениях можно записать так:
, что в принятых обозначениях можно записать так: 
 2020-05-25
2020-05-25 267
267







