Основные формулы дифференцирования:
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
| 14. 
| 15. 
|
Правила дифференцирования:1) 
2) 
3) 


4) 
5) правило дифференцирования сложной функции:  , тогда:
, тогда:  . Производная сложной функции равна произведению производной внешней функции по ее аргументу на производную внутренней функции.
. Производная сложной функции равна произведению производной внешней функции по ее аргументу на производную внутренней функции.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции y = f(x) в точке x, т. е. y / = tg a. Производная есть скорость изменения функции в точке x.
Пример 2. Используя правила и формулы дифференцирования, найти производные функции:  .
.
Решение: 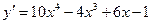 .
.
Пример 3. Используя правила и формулы дифференцирования, найти производные функции: 
Решение. 
Пример 4. Вычислить производную функции y=(3x3-2x+1)×sin x.
Решение. По правилу 3, y'=(3x3-2x+1)'×sin x + (3x3-2x+1)×(sin x)' =
= (9x2-2)sin x + (3x3-2x+1)cos x.
Пример 5. Найти y', y = tg x +  .
.
Решение. Используя правила дифференцирования суммы и частного, получим: y'=(tgx +  )' = (tgx)' + (
)' = (tgx)' + ( )' =
)' =  +
+  =
= 
 .
.
Пример 6. Найти производную сложной функции y =  , u=x4 +1.
, u=x4 +1.
Решение. По правилу дифференцирования сложной функции, получим: y'x =y 'u u'x =( )'u(x4 +1)'x =(2u +
)'u(x4 +1)'x =(2u + 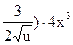 . Так как u=x4 +1,то
. Так как u=x4 +1,то
(2 x4 +2+  .
.
Пример 7. Найти производную функции y=  .
.
Решение. Представим функцию y=  в виде суперпозиции двух функций: y = eu и u = x2. Имеем: y'x =y 'u u'x = (eu)'u(x2)'x = eu ×2x. Подставляя x2 вместо u, получим y=2x
в виде суперпозиции двух функций: y = eu и u = x2. Имеем: y'x =y 'u u'x = (eu)'u(x2)'x = eu ×2x. Подставляя x2 вместо u, получим y=2x  .
.
Пример 8. Найти производную функции y=ln sin x.
Решение. Обозначим u=sin x, тогда производная сложной функции y=ln u вычисляется по формуле y' = (ln u)'u(sin x)'x=  .
.
Индивидуальные домашние задания
Вариант№ 1
Найти производную функции:
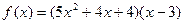




| Вариант№ 5
Найти производную функции:





|
Вариант№ 2
Найти производную функции:





| Вариант№6
Найти производную функции:

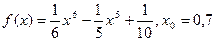



|
Вариант№ 3
Найти производную функции:





| Вариант№ 7
Найти производную функции:





|
Вариант№4
Найти производную функции:

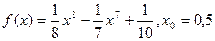


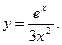
| Вариант№ 8
Найти производную функции:

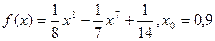


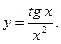
|
 2020-05-25
2020-05-25 229
229







