Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Решите уравнение: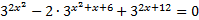

Решение: Запишем уравнение в виде:

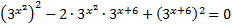
Таким образом, уравнение является однородным относительно функций: и .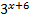

Разделим уравнение на 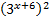и получим:

.

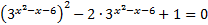Введем новую переменную: .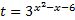

Вспомогательное уравнение:

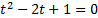
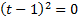
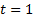
Вернемся к исходной переменной:

.

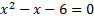
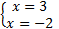Ответ: .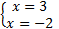

Пример 2.

Решите систему: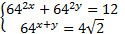

Решение: Введем новые переменные: .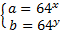

Рассмотрим вспомогательную систему:

.

Возведем второе уравнение в квадрат:

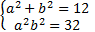. Решим полученную систему относительно и .

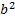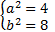или .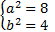

Так как 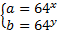, то есть положительные, то

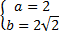или .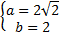

Вернемся к исходным переменным.

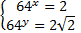или .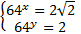

Отсюда:

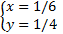или .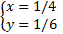

Ответ: (1/6; 1/4); (1/4; 1/6).

Домашнее задание: По задачнику И.М. Башмакова на стр.288 №12.6А (1-3).