План опорного конспекта

Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

План опорного конспекта

Ø Уравнение с двумя переменными и их графическое решение;

Ø Системы уравнений;

Ø Неравенства и их геометрическое решение.

1. Уравнения с двумя переменными и их геометрическое решение.

 

Уравнение вида f(x;y)=0 называется уравнением с двумя переменными.

Решением уравнения с двумя переменными называется упорядоченная пара чисел (α, β), при подстановке которой (α – вместо х, β – вместо  у) в уравнении имеет смысл выражение f( α; β)=0

Решить уравнение – значит найти множество всех его решений.

Уравнения с двумя переменными может:

а) иметь одно решение. Например, уравнение х²+у²=0 имеет одно решение (0;0);

б) иметь несколько решений. Например, данное уравнение (‌‌│ х │- 1)²+(│ у │- 2)²  имеет четыре решения: (1;2),(-1;2),(1;-2),(-1;-2);

в) не иметь решений. Например уравнение х²+у²+ 1=0 не имеет решений;

г) иметь бесконечно много решений. Например, такое уравнение, как х-у+1=0 имеет бесконечно много решений

Иногда бывает полезной геометрическая интерпретация уравнения f(x;y)=g(x;y). На координатной плоскости хОу множество всех решений – некоторое множество точек. В ряде случаев это множество точек есть некоторая линия, и в этом случае говорят, что уравнение f(x;y)=g(x;y) есть уравнение этой линии, например:

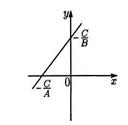
1) уравнение Ах+Ву+С=0 (А²+В² 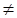0) есть уравнение прямой (рис.1);

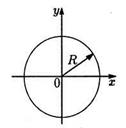
2)  уравнение х²+у²=R² (R 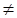0) есть уравнение окружности (рис.2);

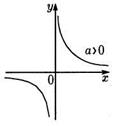
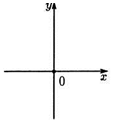
3)  уравнение ху=а (а 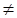0) есть уравнение гиперболы (рис.3,4);

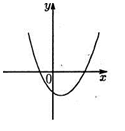
4)  уравнение у=ах²+bх+с (а 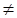0) есть уравнение параболы (рис.5);

5)

 уравнение х²+у²=0 задает одну точку (0;0) (рис.6)

 

                             рис.1                           рис.2                         рис.3

 

 

 

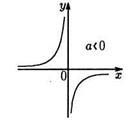рис.4                           рис.5                                   рис.6        

 

                                               

2     Системы уравнений

Пусть заданы два уравнения с неизвестными х и у

                                            F₁(x; y)=0   и   F₂ (x; y)=0

Будем считать, что первое из этих уравнений задаёт на плоскости переменных х и у линию Г₁, а второе - линию Г₂. Чтобы найти точки пересечения этих линий, надо найти все пары чисел (α, β), такие, что при замене в данных уравнениях неизвестной х на число α и неизвестной у на число β, получаются верные числовые равенства. Если поставлена задача об отыскании всех таких пар чисел, то говорят, что требуется решить систему уравнений и записывают эту систему с помощью фигурной скобки в следующем виде

                              

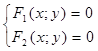
Решением системы называется такая пара чисел (α, β), которая является решением как первого, так и второго уравнений данной системы.

Решить систему – значить найти множество всех ее решений, или доказать, что решений нет.

В ряде случаев геометрическая интерпретация каждого уравнения системы, ибо решения системы соответствуют точкам пересечения линий, задаваемых каждым уравнением системы. Часто геометрическая интерпретация позволяет лишь догадаться о числе решений.

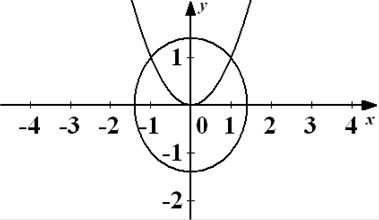
Например, выясним, сколько решений имеет система уравнений

                                        

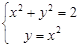
Первое из уравнений системы задает окружность радиусом R= 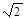 c центром (0;0), а второе – параболу, вершина которой находится в той же точке. Теперь ясно, что имеются две точки пересечения этих линий. Следовательно, система имеет два решения – это (1;1) и (-1;1)

 

 

2.2. Примеры решения уравнений с двумя переменными

 

Изобразите все точки с координатами (х;у), для которых выполняется равенство.

1. (х-1)(2у-3)=0   

Данное уравнение равносильно совокупности двух уравнений

                                                     

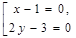
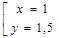
Каждое из полученных уравнений определяет на координатной плоскости прямую.

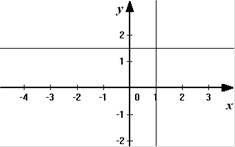
2. (х-у)(х²-4)=0

Решением данного уравнения является множество точек плоскости, координаты, которых удовлетворяют совокупности уравнений

    

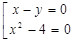
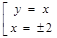
На координатной плоскости решение будет выглядеть так

 

 

 

2.2.Примеры решения систем.

 

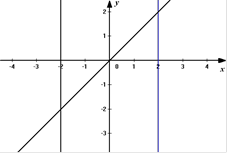
Решить систему графическим способом:

1)                                                                     

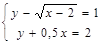
В каждом уравнении выразим переменную у через х и построим графики соответствующих функций:

у = 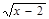+1                                                                                                                          

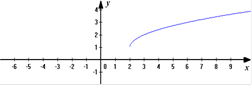
а) построим график функции у=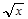      

                                                                                                                                    

 

    

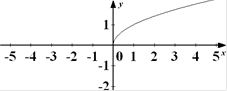
График функции у = 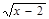+1 получается из графика у = 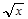путем сдвига на две единицы вправо и на одну единицу вверх:    

у = - 0,5х+2 - это линейная функция, графиком которой является прямая

 

 

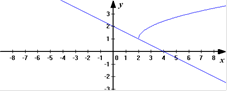
 Решением данной системы являются координаты точки пересечения графиков функций. 

Ответ (2;1)

 

 

3.Неравенства и их геометрическое решение.

Неравенство с двумя неизвестными можно представить так: f(x;y) >0, где Z = f(x;y) – функция двух аргументов х и у. Если мы рассмотрим уравнение f(x;y) = 0, то можно построить его геометрическое изображение, т.е. множество точек М(х;у), координаты которых удовлетворяют этому уравнению. В каждой из областей функция f сохраняет знак, остается выбрать те из них, в которых f(x;у) >0.

Рассмотрим линейное неравенство ax+by+c >0. Если один из коэффициентов a или bотличен от нуля,то уравнение ax+by+c=0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них будет сохраняться знак функции z = ax+by+c. Для определения знака можно взять любую точку полуплоскости и вычислить значение функции z в этой точке.

Например:                        

3 х – 2у +6 >0.

f(x;у) = 3х- 2у +6,

f(-3;0) = -3 <0,

f(0;0) = 6>0.

Решением неравенства является множество точек правой полуплоскости (закрашенной на рисунке 1)

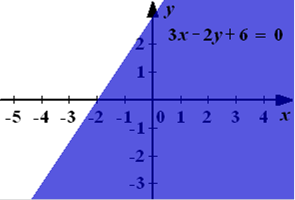
Рис. 1