2020-05-25
405
Пусть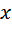 
это время, за которое мастера выполнят работу вместе.
Производительность первого 1/12 (заказа в час), второго 1/6 (заказа в час), этот вывод мы сделали из условия задачи.
При совместной работе производительности складывают.
Оба мастера выполнят заказ за 4 часа.
Ответ: 4
Приложение 2
Рассмотрим разные способы решения иррациональных уравнений:
Иногда помогает область определения функции
1) 
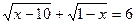
Через ОДЗ. 
Ответ: нет решений.
Бывает полезным использование свойств монотонности функций.
2) 
Корень 3 очевиден. 
и 
- возрастающие функции, поэтому их сумма тоже возрастает. Возрастающая функция достигает каждое свое значение один раз, поэтому больше корней нет.
Ответ: 3
Один из основных методов – замена переменных:
3) 
.
Замена 
. Решаем полученное уравнение и находим 
у1=-4 (иск., у>0), у2=2. 
.
Ответ: 3.
Иногда бывает полезно перейти к системе уравнений:
4) 
Введем переменные: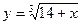 
, 
.
Получаем систему: 
.
|
|
|
После решения системы получим: 
. Возвращаясь к переменной х, получаем ответ: -13 и 13.
Приложение 3
Итоговая контрольная работа
Вариант 1
1. Найти наибольшее и наименьшее значение функции:
на отрезке 
2. Вычислите интеграл: 
3. Решите уравнение:
а) 
б)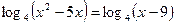 
4. Решите неравенство: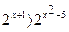 
5. Задача. Измерения прямоугольного параллелепипеда равны 2,5 см, 5 см, 5 см. Найти ребро куба, объем которого в два раза больше объема данного параллелепипеда.
Вариант 2
1. Найти наибольшее и наименьшее значение функции:
на отрезке 
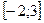
2. Вычислите интеграл: 
3. Решите уравнение:
а) 
б) 
4. Решите неравенство: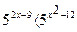 
5. Задача. Измерения прямоугольного параллелепипеда равны 2 см, 6 см, 6 см. Найти ребро куба, объем которого в три раза больше объема данного параллелепипеда.
