Из «А» в «В» одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в «В» одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Примем скорость первого автомобилиста за  км/ч. Расстояние, которое он проезжает от пункта «А» до пункта «В» S(км). Значит время, затраченное им на дорогу
км/ч. Расстояние, которое он проезжает от пункта «А» до пункта «В» S(км). Значит время, затраченное им на дорогу  (ч).
(ч).
Скорость второго на первой половине на 13 км/ч меньше, то есть  (км/ч). На второй половине пути 78 км/ч, значит время, затраченное им на дорогу
(км/ч). На второй половине пути 78 км/ч, значит время, затраченное им на дорогу

Заполним в таблицу:
|
| v | t | S | |
| 1 половина | 2 половина | |||
| 1 |
|  | S | |
| 2 |  | 78 |  | S |
Известно, что в пункт «В» они прибыли одновременно, то есть затратили одинаковое время:

Примечание: в таблице мы записали путь как S. Можно было записать 1, это можно делать, когда не задана длина пути. Суть не меняется (1путь) или (S км) не важно. В уравнении эта величина сократится:






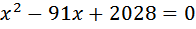
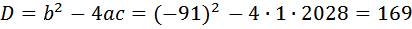


Получили два решения 52 (км/ч) и 39 (км/ч). Но в условии сказано, что искомая скорость больше 48(км/ч).
Ответ: 52
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из «А» в «В» равна х.
Тогда его скорость на обратном пути равна х +7.
Расстояние в обеих строчках таблицы пишем одинаковое: 98 километров. Осталось записать время.  на путь из «А» в «В» велосипедист затратит время
на путь из «А» в «В» велосипедист затратит время  , а на обратный путь время
, а на обратный путь время 
| v | t | S | |
| туда |  |  | 98 |
| обратно |  +7 +7 |  | 98 |
На обратном пути велосипедист сделал остановку на 7 часов и в результате затратил столько же времени, сколько на пути из «А» в «В». Это значит, что на обратном пути он крутил педали (находился в движении) на 7 часов меньше.
Значит,  на семь меньше, чем
на семь меньше, чем  . Получается уравнение:
. Получается уравнение:

Или можно рассудить так: велосипедист на обратный путь затратил
 часов и ещё 7 часов простоял. Очевидно, что уравнение будет иметь вышеуказанный вид.
часов и ещё 7 часов простоял. Очевидно, что уравнение будет иметь вышеуказанный вид.





D=441 

Скорость величина положительная, значит скорость велосипедиста из А в В равна 7 (км/ч).
Ответ: 7
Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Примем скорость второго велосипедиста за х. Тогда скорость первого равна х +3. Расстояние оба проехали одинаковое — 88 километров. Осталось записать время.
Поскольку  , первый затратит
, первый затратит  =
=  часов, а второй
часов, а второй  часов.
часов.
| v | t | S | |
| 1 |  | 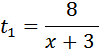 | 88 |
| 2 |  |  | 88 |
Сказано, что первый прибыл на три часа раньше, то есть он затратил время на движение и ещё три часа ожидал, пока прибудет второй. Значит время, затраченное первым на передвижение плюс три часа ожидания второго, равно времени нахождения в пути второго.

Можно рассудить по-другому: выражение «первый прибыл на три часа раньше», означает, что он затратил на пробег на три часа меньше, чем второй. То есть 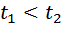 на 3, или
на 3, или
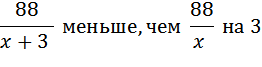

Умножаем левую и правую части на  .
.
Приводим его к квадратному, получим 
Решаем его, получим:
D=361 

 это вполне правдоподобная скорость велосипедиста. А ответ
это вполне правдоподобная скорость велосипедиста. А ответ  не подходит, так как скорость велосипедиста должна быть положительна.
не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: 8
От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью, на 1 км/ч большей, отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Примем скорость первого теплохода за  . Тогда скорость второго теплохода равна
. Тогда скорость второго теплохода равна  .
.
Расстояние оба проехали одинаковое — 420 километров. Осталось записать время.
Поскольку  , первый затратит
, первый затратит  часов, а второй
часов, а второй  часов.
часов.
| v | t | S | |
| 1 |  |  | 420 |
| 2 |  |  | 420 |
Сказано, что через час после отправления первого, в путь отправился второй, то есть он затратил время на движение на час меньше.


Умножаем левую и правую части на  .
.
Приводим к квадратному, получим 
Решаем его: 


Скорость теплохода должна быть положительна, значит, она равна  (км/ч).
(км/ч).
Ответ: 20
Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна  .
.
Тогда скорость движения моторки по течению равна  , а скорость, с которой она движется против течения
, а скорость, с которой она движется против течения  .
.
Расстояние и в ту, и в другую сторону одинаково и равно 255 км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать.
При движении по течению 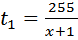 , при движении против течения
, при движении против течения  , причем
, причем  на два часа меньше, чем
на два часа меньше, чем  . Да это и логично, что время на движение по течению затрачивается меньше.
. Да это и логично, что время на движение по течению затрачивается меньше.
| v | t | S | |
| По течению |  |  | 255 |
| Против течения |  |  | 255 |
Условие 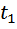 на два часа меньше, чем
на два часа меньше, чем  можно записать в виде
можно записать в виде  .
.



Вообще-то это уравнение имеет два корня: 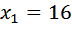 и
и  (оба этих числа при возведении в квадрат дают 256). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
(оба этих числа при возведении в квадрат дают 256). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: 16
Теплоход проходит по течению реки до пункта назначения 216 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 36 часов после отплытия из него. Ответ дайте в км/ч.
От предыдущей эта задача отличается только тем, что нужно найти скорость течения, при известной скорости теплохода. Ход рассуждения тот же.
Скорость течения реки как искомую величину принимаем за x(км/ч). Тогда скорость движения теплохода по течению равна  , а его скорость против течения
, а его скорость против течения  .
.
Расстояние в ту, и в другую сторону одинаковое и равно 216 км.
Всего теплоход затрачивает 36 часов (на весь путь: туда, 6 часов стоянки, обратно).
То есть 36 = время движения по течению + стоянка + время движения против течения.
Занесем скорость и расстояние в таблицу. Заполняем графу «время».
Время, затраченное на путь до пункта назначения  ,
,
Время, затраченное на путь обратно (против течения)  .
.
| v | t | S | |
| По течению |  |  | 216 |
| Против течения |  |  | 216 |
Подставляем данные и получаем уравнение:




Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — раскрываем скобки, складываем подобные члены.
Получаем квадратное уравнение: 
Поскольку скорость течения положительна, получаем: 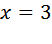 (км/ч).
(км/ч).
Ответ: 3
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Принимаем искомую величину, то есть время, через которое автомобили встретятся за х. В данной задаче проще производить сравнение по расстоянию. Составим таблицу и найдём «расстояние», которое проехал каждый автомобиль.
| v | t | S | |
| 1 |  | x | 65x |
| 2 |  | x | 75 x |
Один проехал до места встречи 65х км, другой 75х км. По условию расстояние между городами 560 км. Значит, сумма пройденных расстояний будет равна 560 км.



Автомобили встретятся через 4 часа.
Ответ: 4
Задачи на работу
Еще один тип задач — это задачи на работу.
Задачи на работу также решаются с помощью одной-единственной формулы:

Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, Вася красит забор. Количество метров, которые он красит за час — это и есть его производительность.
Правила решения задач на работу.
1.  , то есть работа = производительность
, то есть работа = производительность  время. Из этой формулы легко найти t или p.
время. Из этой формулы легко найти t или p.
2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды — работа как раз и равна этому количеству.
3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша...) или трое (не важно) — их производительности складываются. Очень логичное правило.
4. В качестве переменной  удобно взять именно производительность. Так же, как в задах на движение мы за
удобно взять именно производительность. Так же, как в задах на движение мы за  принимаем скорость.
принимаем скорость.
Вы убедитесь, что задачи на работу и движение очень схожи.
РЕШИМ ЗАДАЧИ:
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Как и в задачах на движение, заполним таблицу.
В колонке «работа» и для первого, и для второго рабочего запишем: 110. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем её за  . Тогда производительность первого рабочего равна
. Тогда производительность первого рабочего равна  (он делает на одну деталь в час больше).
(он делает на одну деталь в час больше).
Поскольку  , время работы первого рабочего равно
, время работы первого рабочего равно 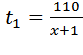 , время работы второго равно
, время работы второго равно  .
.
| p | t | A | |
| 1 рабочий |  |  | 110 |
| 2 рабочий |  |  | 110 |
Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть  на 1 меньше, чем
на 1 меньше, чем  , значит
, значит


Мы уже решали такие уравнения. Оно легко сводится к квадратному:




D=441 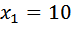

Очевидно, производительность рабочего не может быть отрицательной величиной. Значит, отрицательный корень не подходит.
Ответ: 10
На изготовление 99 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
Данная задача практически не отличается от предыдущей, разница лишь в объёме работы. Примем производительность второго рабочего за  .
.
Тогда производительность первого рабочего равна  (он делает в час на одну деталь больше). Заполним графу «время» в таблице:
(он делает в час на одну деталь больше). Заполним графу «время» в таблице:
| p | t | A | |
| 1 рабочий |  |  | 99 |
| 2 рабочий |  |  | 110 |
Сравнение будем проводить по времени. Сказано, что первый затрачивает на 2 часа меньше, чем второй. Значит


D=961 

Второй рабочий в час делает 10 деталей.
Ответ: 10
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 192 литра она заполняет на 4 минуты дольше, чем вторая труба?
Примем производительность первой трубы за  (литров в минуту). Тогда производительность второй трубы равна
(литров в минуту). Тогда производительность второй трубы равна 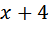 . Работа это объём резервуара – 192 литра. Заполним графу «время» в таблице:
. Работа это объём резервуара – 192 литра. Заполним графу «время» в таблице:
| p | t | A | |
| 1 труба |  |  | 192 |
| 2 труба |  |  | 192 |
Первая труба заполняет резервуар на 4 минуты дольше, чем вторая. То есть времени уходит больше


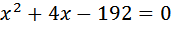
D=784 
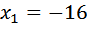
Первая труба в минуту пропускает 12 литров.
Ответ: 12
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Примем производительность первой трубы за  (резервуара в минуту), второй трубы y.
(резервуара в минуту), второй трубы y.
Составим таблицу, для первой и второй трубы заполним графу «время».
Первая труба будет заполнять резервуар  , вторая
, вторая  .
.
| p | t | A | |
| 1 труба |  |  | 1 |
| 2 труба |  |  | 1 |
| обе |  | 4 | 1 |
Первая труба наполняет резервуар на 6 минут дольше, чем вторая, то есть времени затрачивается больше и

Имеем два уравнения, решаем систему

Решение системы сводится к квадратному уравнению, D =100

Получили, что вторая труба заполнит в минуту  резервуара. Тогда весь резервуар будет заполнен за 6 минут.
резервуара. Тогда весь резервуар будет заполнен за 6 минут.
Ответ: 6
В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
Сразу, исходя из условия, можно определить производительности насосов: у первого  (литра в минуту), у второго
(литра в минуту), у второго  (литра в минуту).
(литра в минуту).
Пусть совместно они будут работать  минут.
минут.


Насосы совместно должны работать 6 минут.
Ответ: 6
Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
В данной задаче производительности даны: у Пети 8 (вопросов в час), у Вани 9. Количество вопросов это и есть работа, принимаем за  .
.
В таблице заполним графу «время»:
| p | t | A | |
| Петя | 8 |  |  |
| Ваня | 9 |  |  |
Конечно же, сравнение будем проводить по времени.
Петя закончил свой тест на 20 минут позже Вани, то есть Петя затратил больше времени. Не забываем перевести минуты в часы: 20 минут это 1/3 часа.



Тест содержит 24 вопроса.
Ответ: 24
Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Сразу отметим, что производительность каждого рабочего  (заказа в час). Заказ это работа, она равна 1. Пусть
(заказа в час). Заказ это работа, она равна 1. Пусть  это время совместной работы, тогда один работал
это время совместной работы, тогда один работал  часов, другой
часов, другой  . Заполним графу «работа» для каждого:
. Заполним графу «работа» для каждого:
| p | t | A | |
| 1 рабочий |  |  |  |
| 2 рабочий |  |  |  |
Сумма сделанных ими объёмов работы составляет всю работу, равную 1.


Совместно рабочие работали 6 часов. На весь заказ ушло 
Можно выстроить рассуждение таким образом:
В условии сказано, что рабочий может выполнить заказ за 15 часов, то есть его производительность  заказа в час. Значит, за первые три часа один рабочий выполнит
заказа в час. Значит, за первые три часа один рабочий выполнит  заказа,
заказа,  . Получается, что на двоих останется
. Получается, что на двоих останется  заказа. Далее они работают вдвоём, значит, на каждого из рабочих придётся
заказа. Далее они работают вдвоём, значит, на каждого из рабочих придётся  заказа, так как их производительность одинаковая. Имеем: рабочий выполняет
заказа, так как их производительность одинаковая. Имеем: рабочий выполняет  заказа в час, значит,
заказа в час, значит,  заказа выполнит за 6 часов, то есть совместно они будут работать 6 часов. Итак, на выполнение всего заказа потребуется
заказа выполнит за 6 часов, то есть совместно они будут работать 6 часов. Итак, на выполнение всего заказа потребуется 
Ответ: 9.
 2020-05-25
2020-05-25 804
804







