С. А. МИНАБУДИНОВА, Н. А. ХМЫРОВА, С. В. ВОЗНЮК
КОЛЕБАНИЯ И ВОЛНЫ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ОМСК 2016
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
–––––––––––––––––––––––––––––––––––––
С. А. Минабудинова, Н. А. Хмырова, С. В. Вознюк
КОЛЕБАНИЯ И ВОЛНЫ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Утверждено методическим советом университета
в качестве учебно-методического пособия для самостоятельной работы
студентов при решении задач по физике
Омск 2016
УДК 534(075.8)
ББК 22.236.35я73
М61
Колебания и волны. Примеры решения задач: Учебно-методичес-кое пособие / С. А. Минабудинова, Н. А. Хмырова, С. В. Вознюк; Омский гос. ун-т путей сообщения. Омск, 2016. 36 с.
Учебно-методическое пособие составлено в соответствии с действующей программой по курсу общей физики для вузов, содержит методические рекомендации по изучению физики, примеры решения задач по теме «Колебания и волны». Для решения предлагаемых задач необходимо применить теорию колебаний и волн к гармоническим, затухающим и вынужденным колебаниям механических систем, к электрическому колебательному контуру, механическим и электромагнитным волнам.
Предназначено для студентов 2-го курса очной и заочной форм обучения.
Библиогр.: 8 назв. Рис. 6. Прил. 1.
Рецензенты: канд. филос. наук, доцент Т. В. Добровольская;
канд. техн. наук, доцент Т. В. Ковалева.
__________________________
© Омский гос. университет
путей сообщения, 2016
ОГЛАВЛЕНИЕ
Введение. 5
1. Свободные незатухающие механические колебания. 6
2. Свободные незатухающие колебания в идеальном колебательном контуре. 13
3. Сложение гармонических колебаний. 19
4. Свободные затухающие механические колебания. 22
5. Свободные затухающие колебания в реальном колебательном контуре. 25
6. Плоские монохроматические упругие и электромагнитные волны.. 29
Библиографический список. 34
Приложение. Справочные данные для решения задач. 35

ВВЕДЕНИЕ
Колебательные и волновые процессы наблюдаются в самых разных физических, химических, биологических и других системах. Несмотря на различную природу все они обладают общим признаком – повторяемостью во времени, поэтому и исследуются с единой точки зрения. В теории колебаний общий подход реализуется следующим образом. Независимые характеристики осциллятора (системы, совершающей колебания), описывающие его смещение от положения равновесия, называются обобщенными координатами (число обобщенных координат равно числу колебательных степеней свободы системы). Физические величины – характеристики взаимодействия, приводящего к изменению обобщенных координат системы, рассматриваются как обобщенные силы, действующие на систему, а первые и вторые производные обобщенных координат по времени – соответственно как обобщенные скорости и обобщенные ускорения. Уравнения, описывающие колебания, записываются через обобщенные величины, поэтому вид уравнений определяется только типом колебаний и не зависит от природы осциллятора. Таким образом, осциллятор любой природы описывается моделью материальной точки (частицы), совершающей механические колебания под действием обобщенных сил, а основным математическим аппаратом теории колебаний служат дифференциальные уравнения, структура которых в каждом конкретном случае аналогична структуре основного закона динамики исследуемой (вместо реальной системы) материальной точки.
Так как одной из основных целей издания настоящего учебно-методи-ческого пособия является выработка общего подхода к изучению всевозможных колебательных и волновых явлений, пособие содержит большой набор примеров решения разнообразных задач по теме «Колебания и волны». Для успешного решения приведенных задач требуются теоретические знания и навыки решения задач из других разделов физики. Необходимые теоретические сведения, позволяющие тщательно изучить соответствующую теорию, приведены в литературе [1 – 7]. Структура настоящего издания полностью повторяет структуру пособия [8], в котором приведены задачи для самостоятельной работы студентов.
1. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Как известно, малые свободные незатухающие колебания систем любой природы являются гармоническими. Система, совершающая такие колебания, называется линейным гармоническим осциллятором.
Закон гармонических колебаний имеет вид:
 или
или  .
.
Проекции скорости  и ускорения
и ускорения  на ось
на ось  меняются также по гармоническому закону.
меняются также по гармоническому закону.
Потенциальная и кинетическая энергия механических колебаний вычисляются по формулам:
 и
и  .
.
Полная энергия колебаний не зависит от времени.
П р и м е р 1. Движение материальной точки описывается законом движения:  м. Определить число колебаний, совершенных точкой за 10 с.
м. Определить число колебаний, совершенных точкой за 10 с.
Дано:
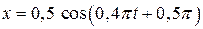 м;
t = 10 с.
Найти: N. м;
t = 10 с.
Найти: N.
|
Решение.
Число колебаний, совершенных точкой за время t, определяется по формуле:
 , (1.1)
, (1.1)
где T – период колебаний (время одного колебания).
Закон движения при гармонических колебаниях точки в общем случае имеет вид:
 , (1.2)
, (1.2)
где w - циклическая частота колебаний, она связана с периодом соотношением:
 . (1.3)
. (1.3)
Из сравнения закона движения (1.2) с законом движения, который дан в условии, видно, что  (с-1). Следовательно, число колебаний за время t
(с-1). Следовательно, число колебаний за время t
 ; (1.4)
; (1.4)
 .
.
Ответ: точка совершит два колебания.
П р и м е р 2. Во сколько раз изменится частота колебаний математи-ческого маятника, если его длину увеличить в четыре раза?
Дано:
 .
Найти: .
Найти:  . .
| Решение.

|
| Рис. 1 |
Частота колебаний математического маятника (рис. 1)
 ,
,
где ℓ - длина математического маятника;
g - ускорение свободного падения
Поэтому
|

 .
.
Ответ: частота колебаний уменьшится в два раза.
П р и м е р 3. Частица массой 14 г совершает свободные незатухающие колебания по закону синуса с периодом 3,7 с и с начальной фазой, равной нулю. Полная энергия колеблющейся частицы – 0,016 мДж. Найти наибольшее значение модуля возвращающей силы, действующей на частицу.
Дано:
 кг; кг;
 с; с;
 ; ;
 ; ;
 Дж.
Найти: Дж.
Найти:  . .
| Решение.
По условию задачи зависимость координаты частицы от времени имеет вид:
 , (1.5)
где , (1.5)
где  – амплитуда; – амплитуда;
 – время; – время;
 - (1.6)
собственная частота колебаний. - (1.6)
собственная частота колебаний.
|
Согласно закону Гука проекция возвращающей силы, действующей на частицу, на ось  вычисляется по формуле:
вычисляется по формуле:
 (1.7)
(1.7)
Так как движение одномерное, модуль силы
 (1.8)
(1.8)
Следовательно, модуль возвращающей силы будет максимален при
 (1.9)
(1.9)
Амплитуда колебаний может быть найдена из выражения для полной энергии
 (1.10)
(1.10)
по формуле:
 (1.11)
(1.11)
Объединив соотношение  и формулу (1.6), получим выражение для расчета обобщенного коэффициента жесткости:
и формулу (1.6), получим выражение для расчета обобщенного коэффициента жесткости:
 . (1.12)
. (1.12)
Подставив равенства (1.9), (1.10) и (1.12) в выражение (1.8), получим максимальное значение модуля возвращающей силы: 
 Отсюда после подстановки данных получим:
Отсюда после подстановки данных получим: 
О т в е т:, 

П р и м е р 4. Математический маятник массой 250 г и длиной 1,2 м совершает гармонические колебания с амплитудой 72 мм. Определить: 1) полную энергию колебаний; 2) модуль скорости колебаний в момент времени, когда смещение маятника от положения равновесия равно 36 мм.
Дано:
 м; м;
 кг; кг;
 м; м;
 м.
Найти: м.
Найти:  ; ; 
| Р е ш е н и е.
1) Полную энергию колебаний маятника вычислим по формуле:
 , (1.13)
подставив в нее соотношение для обобщенного коэффициента жесткости , (1.13)
подставив в нее соотношение для обобщенного коэффициента жесткости
|
 , (1.14)
, (1.14)
а затем – выражение
 (1.15)
(1.15)
для собственной частоты колебаний математического маятника:
 (1.16)
(1.16)
Подставив в формулу (1.16) численные данные, получим: 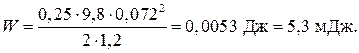
2) Колебания гармонические, поэтому выполняется закон сохранения энергии:
 (1.17)
(1.17)
Полная энергия определяется как сумма потенциальной и кинетической энергий:
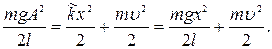 (1.18)
(1.18)
Отсюда в момент времени 
 . (1.19)
. (1.19)
Подставив в формулу (1.19) численные значения всех величин, получим:
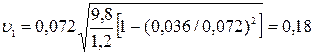 м/с.
м/с.
О т в е т: 
 мДж;
мДж;  ,
, 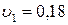 м/с.
м/с.
П р и м е р 5. Материальная точка совершает свободные гармонические колебания вдоль оси  так, что проекция ее скорости на ось
так, что проекция ее скорости на ось  меняется с течением времени по закону:
меняется с течением времени по закону: 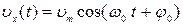 , где
, где 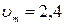 м/с,
м/с,  =
=  рад/с,
рад/с,  Найти момент времени, ближайший к началу колебаний, когда проекция ускорения на ось колебаний
Найти момент времени, ближайший к началу колебаний, когда проекция ускорения на ось колебаний  равна -9,6 м/с2.
равна -9,6 м/с2.
Дано:

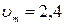 м/с; м/с;
 рад/с; рад/с;
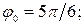
 м/с2.
Найти: м/с2.
Найти: 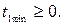
| Р е ш е н и е.
Ускорение можно найти как производную по времени от скорости:
 (1.20)
Выразим фазу колебаний из соотношения (1.20): (1.20)
Выразим фазу колебаний из соотношения (1.20):
 , найдем время: , найдем время:
|
 (1.21)
(1.21)
где  – целое число.
– целое число.
Подстановка численных данных в правую часть формулы (1.21) приводит к ряду значений времени:  распадающемуся на две последовательности, соответствующие двум значениям –
распадающемуся на две последовательности, соответствующие двум значениям –  и
и  – функции
– функции  :
:
 с; (1.22)
с; (1.22)
 с. (1.23)
с. (1.23)
Выбираем из всех возможных решений, представленных последовательностями (1.22) и (1.23), минимальное (ближайшее к нулю) положительное значение времени  с, которое получается при подстановке значения
с, которое получается при подстановке значения  в ряд.
в ряд.
О т в е т: 
 с.
с.
П р и м е р 6. Горизонтальный пружинный маятник массой 170 г выводят из положения равновесия горизонтальным ударом по грузу, после которого маятник начинает совершать гармонические колебания с амплитудой 2 см. Записать закон колебаний и зависимость скорости колебаний от времени, если коэффициент упругости пружины равен 80 Н/м.
Дано:
 кг; кг;
 м; м;
 Н/м; Н/м;
 м.
Найти: м.
Найти:  ; ;  . .
| Р е ш е н и е.
Так как маятник совершает гармонические колебания, зависимость его смещения от положения равновесия от времени в общем случае имеет вид:
 (1.24)
где (1.24)
где  – начальная фаза; – начальная фаза;
|
Собственная частота колебаний маятника
 с. (1.25)
с. (1.25)
Чтобы записать закон движения для рассматриваемого в задаче пружинного маятника в явном виде, необходимо найти начальную фазу колебаний. Для этого подставим в указанный закон начальное условие:  (начальное условие
(начальное условие  м означает, что в момент начала колебаний
м означает, что в момент начала колебаний 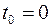 с маятник находился в положении равновесия), откуда
с маятник находился в положении равновесия), откуда
 (1.26)
(1.26)
Подставив соотношение (1.25) и значение начальной фазы (1.26) в закон (1.24), получим зависимость:
 (1.27)
(1.27)
Знак в правой части формулы (1.27) определяется выбором направления оси  вдоль которой происходят колебания маятника. Если, например, направить ось
вдоль которой происходят колебания маятника. Если, например, направить ось  в сторону смещения груза сразу после удара, то сразу после начала колебаний координата груза будет положительной, т. е. зависимость (1.27) примет вид:
в сторону смещения груза сразу после удара, то сразу после начала колебаний координата груза будет положительной, т. е. зависимость (1.27) примет вид:
 (1.28)
(1.28)
где  м;
м; 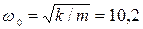 с.
с.
Скорость колебаний можно найти как производную по времени от координаты:
 (1.29)
(1.29)
О т в е т:  где
где  м,
м,  с;
с;
 где
где  м/с.
м/с.
2. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ
В ИДЕАЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Собственная частота колебаний заряда  , силы тока
, силы тока  и напряжения в идеальном колебательном контуре определяется выражением:
и напряжения в идеальном колебательном контуре определяется выражением: 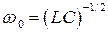 . Заряд совершает гармонические колебания:
. Заряд совершает гармонические колебания:  .
.
Сила тока и напряжение связаны с зарядом соотношениями:  и
и  Энергия электрического и магнитного полей вычисляется по формулам:
Энергия электрического и магнитного полей вычисляется по формулам: 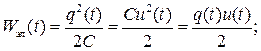

П р и м е р 7. На какую длину волны настроен идеальный колебательный контур, состоящий из катушки индуктивности и конденсатора электроемкостью 6,0 пФ, если максимальный ток в цепи равен 0,1 А, а максимальное напряжение на конденсаторе 2,0 В?
| Дано: I m = 0,1 А; U m = 2,0 В; С = 6,0 пФ. | СИ 0,1 А 2,0 В 6,0×10–12Ф | Решение.
|
| Найти: l. | ||
| Рис. 2 |
Длина волны, на которую настроен идеальный колебательный контур (рис. 2), соответствует собственной частоте контура n и связана с ней соотношением:
 , (2.1)
, (2.1)
где с – скорость света.
Собственная частота колебаний в колебательном контуре
 , (2.2)
, (2.2)
где L и С – индуктивность и электроемкость контура.
Подставив формулу (2.2) в уравнение (2.1), получим:
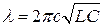 . (2.3)
. (2.3)
Энергия колебаний
 . (2.4)
. (2.4)
Найдем из уравнения (2.4) индуктивность:
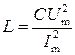 (2.5)
(2.5)
и, подставив выражение (2.5) в формулу (2.3), получим:

 (2.6)
(2.6)
 (м).
(м).
О т в е т: контур настроен на длину волны 22,6 м.
П р и м е р 8. Идеальный колебательный контур состоит из конденсатора емкостью 200 мкФ и катушки индуктивностью 3 мГн. Конденсатор зарядили количеством электричества 70 мкКл и замкнули на катушку. Найти зависимости от времени энергии электрического и магнитного полей.
Дано:
 Ф; Ф;
 мГн; мГн;
 Кл.
Найти: Кл.
Найти:
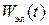 и и 
| Р е ш е н и е.
Энергия электрического и магнитного полей определяется по формулам:
 (2.7) (2.7)
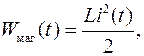 (2.8)
где (2.8)
где  – заряд на пластинах конденсатора; – заряд на пластинах конденсатора;
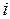 – сила тока, протекающего через катушку. – сила тока, протекающего через катушку.
|
Так как контур идеальный, заряд совершает гармонические колебания:
 (2.9)
(2.9)
где
 (2.10)
(2.10)
собственная частота колебаний в контуре;
 – начальная фаза, определяемая из закона (2.9) при
– начальная фаза, определяемая из закона (2.9) при  с:
с:  , откуда
, откуда
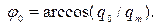 (2.11)
(2.11)
Согласно условию задачи в момент начала колебаний заряженный конденсатор замкнули на катушку, поэтому заряд на пластинах не может быть больше начального. Таким образом, амплитуда колебаний заряда равна начальному заряду:
 (2.12)
(2.12)
Подставив начальное условие (2.12) в формулу (2.11), получим:
 (2.13)
(2.13)
Таким образом, законы (2.9) и (2.7) колебаний заряда и энергии электрического поля в контуре с учетом равенств (2.13) и (2.10) принимают вид:
 (2.14)
(2.14)
 (2.15)
(2.15)
Закон колебаний силы тока найдем, взяв производную по времени от правой части формулы (2.9):
 (2.16)
(2.16)
поэтому зависимость энергии магнитного поля от времени (2.8) с учетом равенств (2.16) и (2.10) принимает вид:
 (2.17)
(2.17)
Зависимости энергии от времени (2.7) и (2.8) представляются в виде:  ;
;  через полную энергию
через полную энергию  мкДж и период колебаний
мкДж и период колебаний  мс.
мс.
О т в е т:  ,
,  ,
,
где  мкДж;
мкДж;  мс.
мс.
П р и м е р 9. В идеальном колебательном контуре с емкостью 6 мкФ заряд на обкладках конденсатора меняется по закону:  где
где  мкКл;
мкКл; 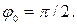 Найти разность потенциалов (напряжение) на обкладках конденсатора спустя четверть периода колебаний.
Найти разность потенциалов (напряжение) на обкладках конденсатора спустя четверть периода колебаний.
Дано:
 Ф; Ф;
  Кл; Кл;
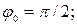
 Найти:
Найти: 
| Р е ш е н и е.
Напряжение связано с зарядом соотношением:  Подставляя в него закон колебаний заряда Подставляя в него закон колебаний заряда 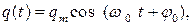 получим зависимость напряжения от времени: получим зависимость напряжения от времени:
 (2.18) (2.18)
|
Выразив в формуле (2.18) собственную частоту колебаний через период  получим:
получим:
 (2.19)
(2.19)
Подставив в формулу (2.19) численные данные при  найдем:
найдем:

О т в е т:  ,
,  В.
В.
П р и м е р 10. В идеальном колебательном контуре с индуктивностью 100 мГн совершаются гармонические колебания с частотой 400 Гц. Найти емкость конденсатора и закон изменения силы тока в контуре, если в начальный момент времени сила тока была максимальной и равной 16 мА.
Дано:
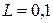 Гн; Гн;
 Гц; Гц;
 А; А;
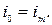 Найти:
Найти:  
| Р е ш е н и е.
Закон колебаний силы тока в идеальном колебательном контуре имеет вид:
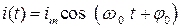 , (2.20)
где , (2.20)
где 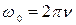 – собственная частота; – собственная частота;
 – начальная фаза колебаний, которая определяется из закона (2.20) при – начальная фаза колебаний, которая определяется из закона (2.20) при 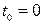 с в соответствии с начальным условием с в соответствии с начальным условием  : :
|
 (2.21)
(2.21)
Подставив выражения (2.21) в закон (2.20), получим зависимость силы тока в рассматриваемом контуре от времени:
 . (2.22)
. (2.22)
Емкость конденсатора найдем из выражения  :
:
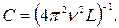 (2.23)
(2.23)
Отсюда 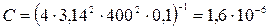 Ф.
Ф.
О т в е т:  мА;
мА; 
 мкФ.
мкФ.
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
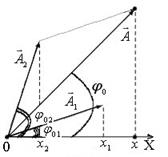
При сложении гармонических колебаний одного направления и одинаковой частоты удобно использовать метод векторных диаграмм (рис. 3).
|
| Рис. 3 |
Вектор 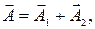 описывающий результирующее колебание, строится по правилам сложения векторов.
описывающий результирующее колебание, строится по правилам сложения векторов.
Амплитуда и начальная фаза результирующего колебания определяются по диаграмме для начального момента времени (см. рис. 3), их значения вычисляются соответственно по формулам:


При сложении гармонических взаимно перпендикулярных колебаний, совершаемых точкой в плоскости  , необходимо найти уравнение траектории, иск-лючив из закона колебания время, например, выразить
, необходимо найти уравнение траектории, иск-лючив из закона колебания время, например, выразить  через
через  или
или  .
.
Если при этом отношение частот (периодов)  является рациональной дробью (отношением целых чисел), то траектория оказывается замк-нутой, а движение – периодическим.
является рациональной дробью (отношением целых чисел), то траектория оказывается замк-нутой, а движение – периодическим.
П р и м е р 11. Построить векторную диаграмму в начальный момент времени при сложении двух гармонических колебаний одинаковой частоты и одного направления. Найти графически и аналитически амплитуду и начальную фазу результирующего колебания. Записать закон результирующего колебания. Законы складываемых колебаний имеют вид: 
 где
где  см;
см;  см;
см;  с-1;
с-1; 

Дано:


 с-1; с-1;
 см; см;  см; см;
 ; ;  Найти:
Найти:  ; ;  
| Р е ш е н и е.
Чтобы найти амплитуду и начальную фазу результирующего колебания, можно воспользоваться формулами для амплитуды и начальной фазы результирующего колебания, предварительно заменив по формуле приведения  синусоидальную зависимость синусоидальную зависимость  косинусоидальной: косинусоидальной:
 (3.1)
где (3.1)
где
|
 (3.2)
(3.2)
Тогда
 . (3.3)
. (3.3)
Подставляя в равенства (3.3) численные данные и учитывая формулу (3.2), получим:  см;
см; 
Отсюда  °
°  рад. Следовательно, закон результирующего колебания имеет вид:
рад. Следовательно, закон результирующего колебания имеет вид:  где
где  см;
см;  с-1;
с-1;  рад.
рад.
Начертим векторную диаграмму сложения колебаний в начальный момент времени (рис. 4). Для этого в соответствии с правилами построения сопос-тавим колебанию  вектор
вектор  длиной
длиной  , который направим под углом
, который направим под углом 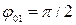 к горизонтальной оси
к горизонтальной оси  , т. е. вертикально вверх; колебанию
, т. е. вертикально вверх; колебанию  со-
со-

|
| Рис.4 |
поставим вектор  длиной
длиной  , который направим под углом
, который направим под углом  к горизонтальной оси
к горизонтальной оси  , т. е. отложим его в направлении оси (см. рис. 4). Результирующее колебание будет описываться вектором
, т. е. отложим его в направлении оси (см. рис. 4). Результирующее колебание будет описываться вектором 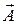 длиной
длиной 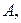 полученным по правилу параллелограмма сложением векторов
полученным по правилу параллелограмма сложением векторов 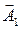 и
и 
Угол, образованный вектором 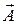 и осью
и осью  равен начальной фазе результирующего колебания
равен начальной фазе результирующего колебания 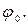
О т в е т:  где
где  см;
см;  с-1
с-1  рад.
рад.
П р и м е р 12. Получить уравнение траектории частицы и построить траекторию в плоскости  , если частица одновременно участвует в двух взаимно перпендикулярных колебаниях:
, если частица одновременно участвует в двух взаимно перпендикулярных колебаниях: 
 где
где  см,
см, 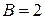 см.
см.
Дано:

 Найти:
Найти: 
| Р е ш е н и е.
Чтобы найти уравнение траектории точки  на плоскости на плоскости 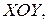 необходимо из сис-темы уравнений необходимо из сис-темы уравнений
|
 (3.4)
(3.4)
 (3.5)
(3.5)
исключить время. Для этого из уравнения (3.4) выразим 
 . (3.6)
. (3.6)
Отсюда
 . (3.7)
. (3.7)
Преобразовав и возведя в квадрат уравнение (3.5) и последовательно применив формулы приведения и двойного аргумента к тригонометрическим функциям, получим:
 . (3.8)
. (3.8)
Используя соотношения (3.6) и (3.7), из выражения (3.8) можно исключить время и получить уравнение траектории:
 (3.9)
(3.9)
 Для построения траектории в плоскости
Для построения траектории в плоскости  выберем наиболее удобные точки.
выберем наиболее удобные точки.
Это точки, имеющие равную нулю, наибольшую и наименьшую из возможных ординату ( ) или абсциссу (
) или абсциссу ( ).
).
| 
|

| 
|

| 
|
Используя уравнение траектории (3.9), найдем вторые координаты этих точек (таблица).
Траектория, построенная по этим точкам, показана на рис. 5. Координата  достигает максимума по модулю четырежды, а
достигает максимума по модулю четырежды, а 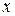 – дважды. Это объясняется соответствующим отношением частот: за время одного колебания вдоль оси
– дважды. Это объясняется соответствующим отношением частот: за время одного колебания вдоль оси  точка совершает два колебания вдоль оси
точка совершает два колебания вдоль оси 
О т в е т: 
 2020-05-21
2020-05-21 394
394








