Пусть плоская монохроматическая (гармоническая) волна с длиной  и периодом
и периодом  распространяется в направлении оси
распространяется в направлении оси  с (фазовой) скоростью
с (фазовой) скоростью  Тогда уравнение, описывающее колебания точек такой волны (уравнение бегущей волны), имеет вид:
Тогда уравнение, описывающее колебания точек такой волны (уравнение бегущей волны), имеет вид:  .
.
Разность фаз гармонической волны в двух точках с координатами  и
и 
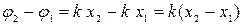 .
.

|
| Рис. 6 |
В плоской монохроматической электромагнитной волне, распространяющейся вдоль оси  в однородной изотропной среде, направления колебаний векторов напряженностей электрического
в однородной изотропной среде, направления колебаний векторов напряженностей электрического  и магнитного
и магнитного  полей в любой момент времени перпендикулярны направлению распространения волны (рис. 6). Законы колебаний проекций векторов
полей в любой момент времени перпендикулярны направлению распространения волны (рис. 6). Законы колебаний проекций векторов  и
и  во всех точках с координатой
во всех точках с координатой  имеют вид:
имеют вид:
 ;
; 
и связаны между собой соотношением: 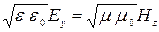 . Частоты и фазы колебаний напряженности электрического и магнитного полей плоской монохроматической электромагнитной волны одинаковы в любой момент времени. Максимальная скорость распространения электромагнитных волн – их скорость в вакууме, равная скорости света в вакууме:
. Частоты и фазы колебаний напряженности электрического и магнитного полей плоской монохроматической электромагнитной волны одинаковы в любой момент времени. Максимальная скорость распространения электромагнитных волн – их скорость в вакууме, равная скорости света в вакууме:  м/с.
м/с.
П р и м е р 17. В упругой среде вдоль оси  распространяется плоская гармоническая волна от источника, совершающего колебания по закону:
распространяется плоская гармоническая волна от источника, совершающего колебания по закону:  где
где  мкм;
мкм;  с-1;
с-1;  Скорость распространения волны 75 м/с. В начальный момент времени смещение источника колебаний от положения равновесия имело максимальное по модулю отрицательно значение. Найти: 1) волновое число; 2) длину волны; 3) скорость колебаний частиц, расположенных на расстоянии 1125 м от источника спустя 15 с от начала колебаний; 4) разность фаз колебаний двух точек, лежащих на одном луче, до которых волна доходит соответственно через 24 и 33 c от начала колебаний источника.
Скорость распространения волны 75 м/с. В начальный момент времени смещение источника колебаний от положения равновесия имело максимальное по модулю отрицательно значение. Найти: 1) волновое число; 2) длину волны; 3) скорость колебаний частиц, расположенных на расстоянии 1125 м от источника спустя 15 с от начала колебаний; 4) разность фаз колебаний двух точек, лежащих на одном луче, до которых волна доходит соответственно через 24 и 33 c от начала колебаний источника.
Дано:

 м; м;
 с-1; с-1;
 ; ;
 м/с; м/с;
 м; м;
 с; с;
 с; с;
 с.
Найти: с.
Найти:  
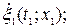 
| Р е ш е н и е.
Волновое число связано с циклической частотой колебаний, скоростью и длиной волны соотношением:
 (6.1)
Отсюда длина волны (6.1)
Отсюда длина волны
 (6.2)
Уравнение плоской бегущей в направлении оси (6.2)
Уравнение плоской бегущей в направлении оси  волны с учетом выражения (6.1) имеет вид: волны с учетом выражения (6.1) имеет вид:
 . (6.3) . (6.3)
|
Скорость колебаний частиц в любой точке волны можно найти, продифференцировав закон (6.3):
 (6.4)
(6.4)
Следовательно, скорость колебаний частиц в точке волны с координатой  в момент времени
в момент времени  определяется равенством:
определяется равенством:
 . (6.5)
. (6.5)
За время  волна, движущаяся с постоянной скоростью, достигает точки с координатой
волна, движущаяся с постоянной скоростью, достигает точки с координатой
 (6.6)
(6.6)
Отсюда
 (6.7)
(6.7)
Фаза волны в рассматриваемом случае 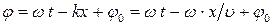 . Следовательно, в любой фиксированный момент времени
. Следовательно, в любой фиксированный момент времени  разность фаз колебаний в точках с координатами
разность фаз колебаний в точках с координатами 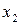 и
и  можно вычислить по формуле:
можно вычислить по формуле:
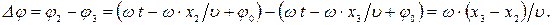 (6.8)
(6.8)
Если подставить в формулу (6.1) значения координат колеблющихся точек (6.3), то получим расчетную формулу для разности фаз:
 . (6.9)
. (6.9)
Подставляем в выражения (6.1), (6.2), (6.5) и (6.9) численные данные:
 м-1;
м-1;
 м;
м;
 м;
м;
 рад, следовательно, эти точки колеблются в одной фазе.
рад, следовательно, эти точки колеблются в одной фазе.
О т в е т:  ,
,  м-1;
м-1;
 ,
,  м;
м;
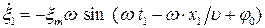 ,
,  м;
м;
 ,
,  , т. е. точки колеблются в одной фазе.
, т. е. точки колеблются в одной фазе.
П р и м е р 18. Плоская электромагнитная волна распространяется вдоль оси  в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 2,3. Частота, амплитуда и начальная фаза колебаний напряженности магнитного поля соответственно равны 4,1·107 Гц, 7,8·103 А/м и
в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 2,3. Частота, амплитуда и начальная фаза колебаний напряженности магнитного поля соответственно равны 4,1·107 Гц, 7,8·103 А/м и  Найти: 1) длину волны в вакууме и в данной среде; 2) напряженность электрического поля в точках, расположенных на расстоянии 3,2 м от источника, в момент времени, равный половине периода.
Найти: 1) длину волны в вакууме и в данной среде; 2) напряженность электрического поля в точках, расположенных на расстоянии 3,2 м от источника, в момент времени, равный половине периода.
Дано:
 ; ; 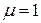 ; ;
 Гц; Гц;
 А/м; А/м;
 ; ;
 Ф/м; Ф/м;
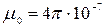 Гн/м; Гн/м;
 м/с; м/с;
 м; м;  Найти:
Найти:  ; ;  ; ; 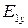 . .
| Р е ш е н и е.
Длина волны связана с частотой и скоростью распространения соотношением:
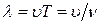 . (6.10)
Скорость распространения электромагнитной волны в вакууме . (6.10)
Скорость распространения электромагнитной волны в вакууме  , в среде – , в среде –
 , (6.11)
поэтому значения длины волны в вакууме и в среде вычисляются по формулам: , (6.11)
поэтому значения длины волны в вакууме и в среде вычисляются по формулам:
|
 ;
;  . (6.12)
. (6.12)
Подставив в соотношения (6.12) численные данные, получим:
 м;
м;  м.
м.
Напряженность электрического поля  (см. рис. 6), где
(см. рис. 6), где
 . (6.13)
. (6.13)
Амплитуду колебаний напряженности электрического поля найдем, пользуясь соотношением  :
:
 . (6.14)
. (6.14)
Циклическую частоту и волновое число найдем, пользуясь соответствующими определениями и формулой (6.11):
 ; (6.15)
; (6.15)
 . (6.16)
. (6.16)
С учетом выражений (6.14) – (6.16) формула (6.13) принимает вид:
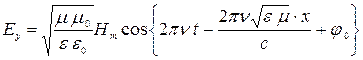 . (6.17)
. (6.17)
Подставив в соотношение (6.17) численные данные, получим при  (с учетом равенства
(с учетом равенства  ) и
) и 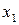 :
:
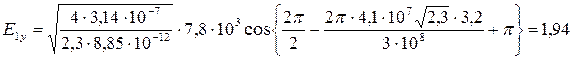 МВ/м.
МВ/м.
О т в е т:  ,
, 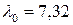 м;
м;
 ,
,  м;
м;

 МВ/м.
МВ/м.
 2020-05-21
2020-05-21 203
203








