Математическая постановка задачи

Законченная концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, включающую совокупность различных математических соотношений, описывающих поведение и свойства объекта моделирования.

Математическая постановка задачи моделирования (математическая модель) - это совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

Математическая постановка задачи баскетболиста основана на втором законе Ньютона. Согласно этому закону, уравнение движения материальной точки в поле силы тяжести (простейшая базовая модель) имеет следующий вид:

,                               (2.1)

где  - масса мяча, 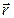 - радиус-вектор центра масс мяча,  - скорость мяча,  - ускорение свободного падения (в полете на мяч действует только сила тяжести).

Уравнение (2.1) является дифференциальным, поэтому для его решения необходимо задать начальные условия (в нашем случае):

и .                              (2.2)

Приведенные начальные условия означают, что в начальный момент времени мяч расположен в начале координат выбранной системы отсчета, и его вектор скорости известен.

Смещение центра мяча от центра кольца, влияющее на точность (результативность) броска, вычисляем по формуле:

,                                               (2.3)

где 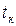 - время полета мяча к центру корзины, имеющего координаты .

При решении уравнения (2.1) необходимо учесть условия попадания мяча в кольцо (см. концептуальную модель):

.                          (2.4)

Проецируя векторные соотношения (2.1) - (2.4) на оси декартовой системы координат с началом отсчета, совпадающим с положением баскетболиста в момент броска, получим математическую постановку задачи в координатной форме:

1. Найти зависимости путем решения системы дифференциальных уравнений первого порядка:

               (2.5)

при следующих начальных условиях:

     (2.6)

2. Вычислить параметр по формуле

                                       (2.7)

где  - определить из условий

.                          (2.8)

3. Оценить результативность броска.

Как можно видеть, с математической точки зрения задача баскетболиста свелась к задаче Коши для системы ОДУ первого порядка с заданными начальными условиями. Полученная система уравнений является замкнутой, так как число независимых уравнений (четыре дифференциальных и два алгебраических) равно числу искомых параметров задачи .

По уравнениям (2.5) легко проверить контроль физических размерностей параметров задачи.

Существование и единственность решения задачи Коши доказана математиками. Поэтому данную математическую модель можно считать корректной.

Математическая постановка задачи еще более абстрактна, чем концептуальная, так как сводит исходную задачу к чисто математической (в данном случае, к задаче Коши), методы решения которой достаточно хорошо разработаны. Умение свести исходную проблему к известному классу математических задач и обосновать правомочность такого сведения требует высокой квалификации системного аналитика (прикладного математика, расчетчика).

Поиск решения задачи сводится к отысканию некоторых зависимостей искомых, величин от исходных параметров модели. Как было отмечено выше, все методы решения задач, составляющих «ядро» математических моделей, можно разделить на аналитические и алгоритмические.

Следует отметить, что при использовании аналитических решений для получения результатов «в числах» также часто требуется разработка соответствующих алгоритмов, реализуемых на ЭВМ. Однако исходное решение при этом представляет собой аналитическое выражение (или их совокупность). Решения же, основанные на алгоритмических методах, принципиально не сводимы к точным аналитическим решениям рассматриваемой задачи.

Как уже было отмечено, аналитические методы более удобны для последующего анализа результатов, но применимы лишь для относительно простых моделей. В случае, если математическая задача (хотя бы и в упрошенной постановке) допускает аналитическое решение, последнее, без сомнения, предпочтительнее численного.

Алгоритмические методы сводятся к некоторому алгоритму, реализующему вычислительный эксперимент с использованием ЭВМ. Точность моделирования в подобном эксперименте существенно зависит от выбранного метода и его параметров (например, шага интегрирования). Алгоритмические методы, как правило, более трудоемки в реализации, требуют хорошего знания методов вычислительной математики, обширной библиотеки специального программного обеспечения и мощной вычислительной техники.