Метод наименьшего элемента

Сущность метода в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.

Пример 2: Составить опорный план задачи методом наименьшего элемента.

Решение: Исходная транспортная таблица имеет вид:

Построим опорный план.

Находим в таблице наименьшую стоимость перевозки – это 0 в клетке A1B2. Записываем в этой клетке значение 12 (наименьшее из сумм по строке и столбцу).

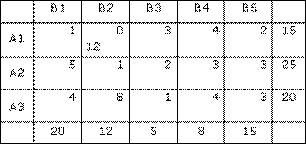
Теперь вычеркиваем второй столбец, уменьшив сумму в первой строке на 12.

Находим следующую наименьшую по стоимости ячейку – их несколько, например, A1B1. Присваиваем ей значение 3, а сумму по столбцу заменяем на 17.

Вычеркиваем первую строку.

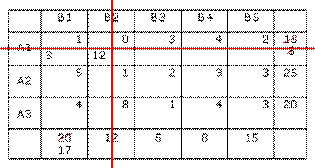
Выбираем ячейку A3B3, присваиваем ей значение 5. Вычеркиваем третий столбец. Сумму по третьей строке заменяем на 15.

Выбираем ячейку A2B5, записываем в ней 15, уменьшаем вторую строку на 15 и вычеркиваем пятый столбец.

Выбираем ячейку A3B1, присваиваем ей 15. Уменьшаем первый столбец на 15 и вычеркиваем третью строку.

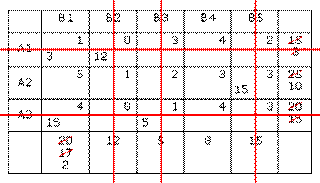
Ячейке A2B1 присваиваем 2 и вычеркиваем первый столбец. Сумму по второй строке заменяем на 8.

Ячейке A2B4 присваиваем 8 и вычеркиваем четвертый столбец.

Опорный план построен.

Количество заполненных клеток 3+5-1=7.

Х₁₁ = 3, Х₁₂ = 12, Х₂₁ = 2, Х₂₄ = 8, Х₂₅ = 15, Х₃₁ = 15, Х₃₃ = 5.

Все остальные Х_ij = 0.

Вычислим суммарную стоимость перевозок для построенного плана:

F = 3*1+0*12+5*2+3*8+3*15+5*1 = 147.

147>136, т.е. данный план точно не оптимальный.

Итак, мы изучили 2 способа построения первого опорного плана. При решении задачи вы выбираете тот способ, который вам больше понравился (более понятен).

Теперь необходимо проверить, будет ли построенный план оптимальным, т.е. получим ли мы минимальную стоимость перевозок.

Для этого воспользуемся методом потенциалов.