Математическая модель транспортной задачи

Лекция № 14.

Тема. Транспортная задача. Постановка задачи. Методы решения

План

1. Введение.

2. Постановка транспортной задачи.

3. Методы решения транспортных задач.

4. Метод потенциалов решения транспортных задач.

Введение.

На прошлой лекции мы рассмотрели общие подходы к решению задач линейного программирования. Однако существуют частные типы задач линейного программирования, которые в силу своей структуры допускают решения более простыми методами. Сегодня мы остановимся на одной из них – так называемой, транспортной задаче.

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью.

Мы рассмотрим классическую транспортную задачу – это задача об оптимальном плане перевозок продукта(-ов) из пунктов отправления в пункты потребления, встречается чаще всего в практических приложениях линейного программирования.

Где могут пригодиться вам полученные сегодня знания.

На каждом предприятии есть отдел логистики. Его работа заключается в организации рационального процесса продвижения товаров от производителей к потребителям, создания инфраструктуры товародвижения.

Логисты обязательно должны уметь работать в Word, Excel, Access. Так как все эти знания вы имеете, то вполне можете работать логистами в дальнейшем.

Целью лекции является: постановка транспортной задачи,  построение математической модели этой задачи и ее решение.

Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.

В 1975 году академик Л.В.Канторович и американец профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за “вклад в разработку теории и оптимального использования ресурсов в экономике”.

Постановка транспортной задачи

Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2,..., Аm соответственно в количествах а1, а2,..., аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2,..., Вn соответственно в количествах b1, b2,..., bn единиц. Стоимость перевозки (тариф) единицы продукции из Аi в Вj известна для всех маршрутов Ai, Bj и равна c_ij (i = 1, m; j = 1, n).

Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится, и запросы всех пунктов потребления удовлетворяются, а суммарные транспортные расходы минимальны.

Замечание:

Задача в данной формулировке, когда выполняется равенство

 

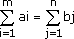
называется закрытой.

Чтобы мы могли решать данную задачу нам необходимо записать ее математическую модель.

Математическая модель транспортной задачи

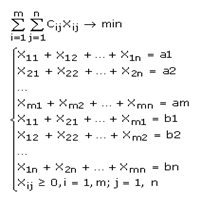
Наша задача найти значения х, которые удовлетворяют системе ограничений и целевой функции.

При этом нам понадобятся несколько определений:

Определение: Построенный план называется опорным, если в нем отличны от нуля m+n-1 базисных перевозок, а остальные перевозки равны 0.

Определение: Опорный план называется оптимальным, если он приводит к минимальной суммарной стоимости перевозок.