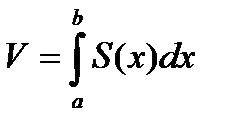Группа 314 Дата 29.04
| Тема: | «Применение определенного интеграла для вычисления геометрических и физических величин» |
| Цель урока: | Показать применение интеграла в решении задач на нахождение объемов тел вращения, решении физических задач. |
Тип: обобщения и систематизации, лекция.
Ход урока.
- Организационный момент.
- Повторение ранее изученного.
А) Вычисление объемов тел
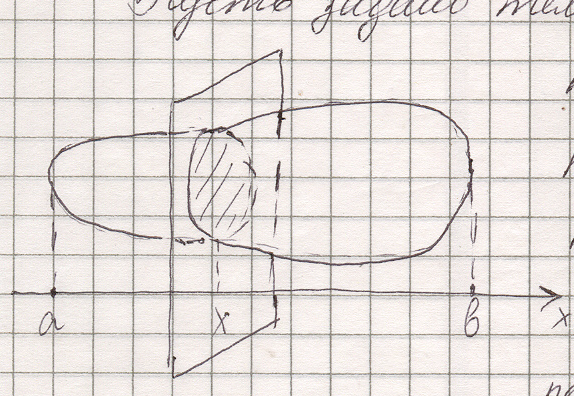
| Пусть задано тело объемом V, причем имеется такая прямая, что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадьS сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох пересекает ее в некоторой точке х. Следовательно, каждому числу xÎ[a;b] поставлено в соответствие единственное число S(x) – площадь |
| сечения тела этой плоскостью. Тем самым на отрезке [a;b] задана функция S(x). Если функция S непрерывна на отрезке [a;b], то справедлива формула
| |
Разобьем отрезок [a;b] на n отрезков равной длины точками
x = a< x1< x2< … < xn-1< b = xn, и пусть
D x = 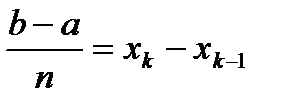 , k = 1, 2, …,n
, k = 1, 2, …,n
 Через каждую точку xk проведем плоскость, перпендикулярную оси 0х. Эти плоскости разрезают заданное тело на слои.
Через каждую точку xk проведем плоскость, перпендикулярную оси 0х. Эти плоскости разрезают заданное тело на слои.
Объем слоя, заключенного между плоскостями 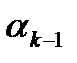 и
и  , при достаточно больших n приближенно равен площади S(xk-1) сечения, умноженной на «толщину слоя» D x, и поэтому V
, при достаточно больших n приближенно равен площади S(xk-1) сечения, умноженной на «толщину слоя» D x, и поэтому V 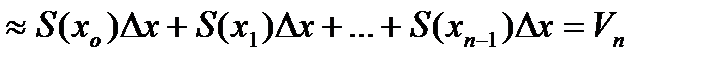
Точность этого приближенного равенства тем выше, чем тоньше слои, на которые порезано тело, т.е. чем больше n. Поэтому Vn®V при n®¥. По определению интеграла Vn® 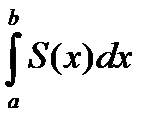 при n®¥.
при n®¥.
Пример 1.
Доказать, что объем усеченной пирамиды с высотой Н и с площадями оснований S и s равен
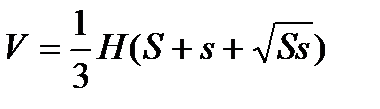
Доказательство.
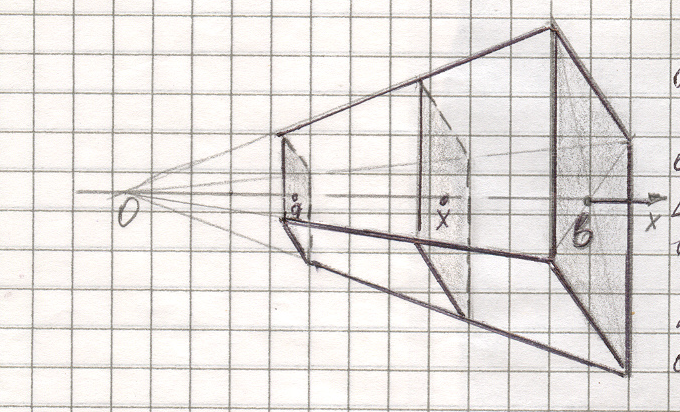
| Пусть точка О – вершина «полной» пирамиды. Ось 0х перпендикулярна основанию пирамиды. Основания усеченной пирамиды пересекают ось 0х в точках a и b. Каждая плоскость, перпендикулярная оси 0х и пересекающая отрезок [a;b] этой оси в точке х дает в сечении многоугольник, подобный многоугольнику – основанию пирамиды. Поэтому площадь сечения S(x) = kx2 |
S = S(a) = ka2 и S = S(b) = kb2
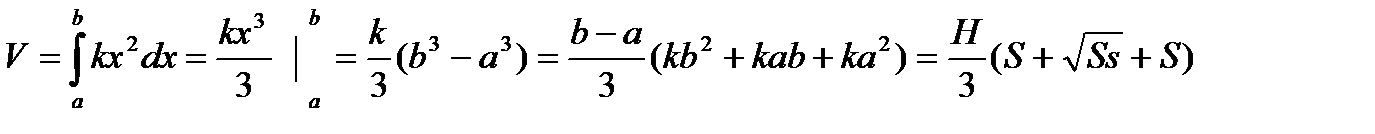
.
Пример 2.
Пусть криволинейная трапеция опирается на отрезок [a;b] оси 0х и ограничена сверху графиком функции f, неотрицательной и непрерывной на отрезке [a;b].
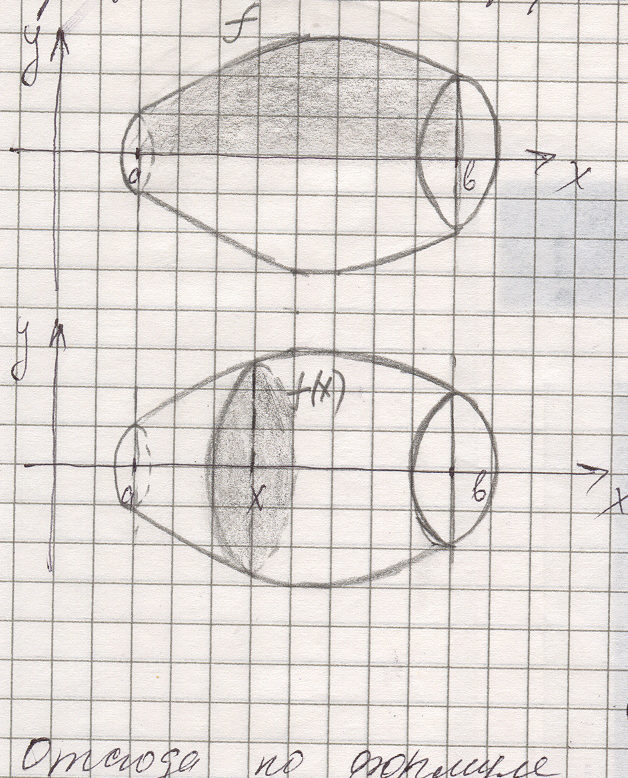
| При вращении этой криволинейной трапеции вокруг оси 0х получаем тело, объем которого находится по формуле 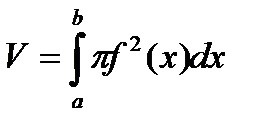 Действительно, каждая плоскость, перпендикулярная оси 0х и пересекающая отрезок [a;b] этой оси в точке х, дает в сечении с телом круг радиуса f(x) и площади S(x) = p f 2(x). Отсюда по формуле Действительно, каждая плоскость, перпендикулярная оси 0х и пересекающая отрезок [a;b] этой оси в точке х, дает в сечении с телом круг радиуса f(x) и площади S(x) = p f 2(x). Отсюда по формуле
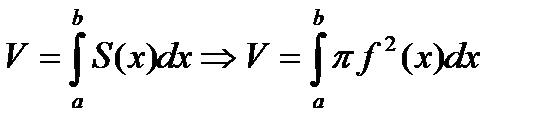
|
б) Работа переменной силы
Рассмотрим материальную точку, движущуюся под действием силы P по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещении равно S, то работа А этой силы равна произведению Ps.
Выведем формулу для подсчета работы, совершаемой переменной силой.
Пусть точка движется по оси 0х под действием силы, проекция которой на ось 0х есть функция f от х. При этом будем полагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М(а) в точку М(b).
| 0 а b х |
| М(а) М(b) |
Покажем, что в этом случае работа А подсчитывается по формуле 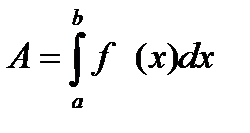 . Разобьем отрезок [a;b] на n отрезков одинаковой длины D x =
. Разобьем отрезок [a;b] на n отрезков одинаковой длины D x = 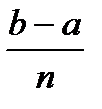
Это отрезки [a;x1]; [x1;x2];…; [xn-1;b]
| х |
| 0 а=хо х1 х2 хn-1 b= хn |
| М(а) М(b) |
Работа силы на всем отрезке [a;b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от х, при достаточно малом отрезке [a;x1] работа силы на этом отрезке приблизительно равна f(a) [x1-a]. Мы пренебрегли тем, что f на отрезке меняется. Аналогично работа силы на втором отрезке [x1; x2] приближенно равна f(x1) (x1-x2) и т.д.;работа силы на отрезке приближенно равна. Следовательно, работа силы на n-м отрезке приближенна равна f(xn-1) (b-xn-1). Следовательно, работа силы на всем отрезке [a;b] приближенно равна:

и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [a;b]. Это равенство переходит в точное, если считать, что n®¥.
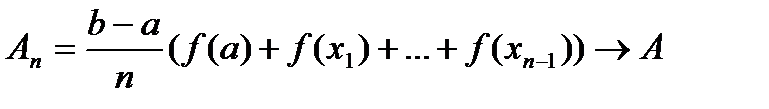
Т.к. 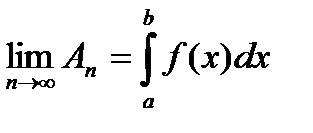 , то формула выведена.
, то формула выведена.
Пример 3
Сила упругости пружины, растянутой на 5 см, равна 3Н. Какую работу надо произвести, чтобы растянуть пружину на 5 см?
Решение.
По закону Гука сила F, растягивающая пружину на величину х, вычисляется по формуле F = kx, где k – постоянный коэффициент пропорциональности, точка 0 соответствует свободному положению пружины.
| х |
| 0 |
| х |
| 0 |
| х |
Из условия задачи следует, что 3 = k . 0,05Þ k=60 и F=60х.
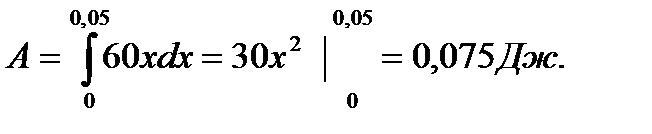
В) Центр масс.
При нахождении центра масс пользуются следующими правилами:
1) Координата х¢ центра масс системы материальных точек А1, А2. …, Аn с массами m1, m2, …, mn, расположенных на прямой в точках с координатами х1, х2, …, хn, находится по формуле:
х¢ = 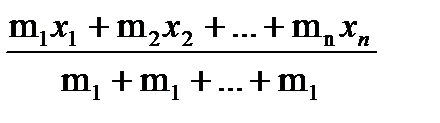
2) При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры.
Пример 4.
Пусть вдоль стержня – отрезка [a;b]. оси 0х – распределена масса плотностью r(х), где r(х) непрерывная функция. Покажем, что:
а) суммарная масса стержня 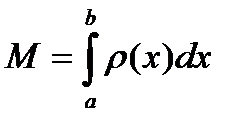
б) координата центра масс х¢ = 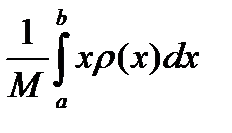
Разобьем отрезок [a;b] на n равных частей точками a=xо< x1< x2<… < xn= b
| 0 а=хо х1 х2 хn-1 b- хn |
| М(а) М(b) |
| х |
На каждом из n этих отрезков плотность можно считать при больших n постоянной и примерно равной r(хk-1) на k-м отрезке (в силу непрерывности r(х)).
Тогда масса k-го отрезка примерно равна
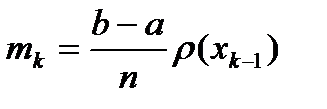 , а масса всего стержня равна
, а масса всего стержня равна 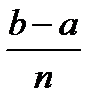 (r(хо)+ r(х1)+…+ r(хn+1))
(r(хо)+ r(х1)+…+ r(хn+1))
Считая каждый из n маленьких отрезков материальной точкой массы 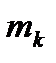 , помещенной в точке
, помещенной в точке 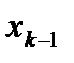 , получим по формуле, что координата центра масс приближенно находится так:
, получим по формуле, что координата центра масс приближенно находится так:
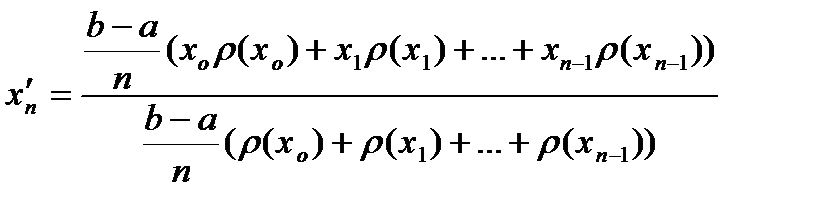
При n®¥. Числитель стремится к 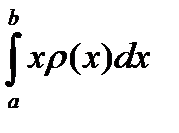 , а знаменатель (выражающий массу всего стержня) к интегралу
, а знаменатель (выражающий массу всего стержня) к интегралу 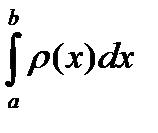 .
.
 2020-06-08
2020-06-08 221
221