Лекция Выявление различий в распределении признака 29.04

1. Задачи сравнения распределений признака в психологии

2. Критерий c² Пирсона

3. Критерий l Колмогорова – Смирнова

 

1. Распределения признаков могут различаться как по своим числовым характеристикам (средняя выборочная, дисперсия, асимметрия, эксцесс и т.п.) так и по сочетаниям этих характеристик. Приведем два примера.

  Пример 1. Рассмотрим (рис.4.1) два нормальных распределения признака с общим средним 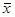 и различными дисперсиями, кроме того, у первого распределения эксцесс положительный, у второго – отрицательный. Тогда первое распределение характеризуется меньшим диапазоном вариативности, то есть в нем чаще встречаются значения признака, близкие к среднему 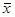, тогда как во втором распределении чаще встречаются более низкие и более высокие значения, чем .

            

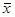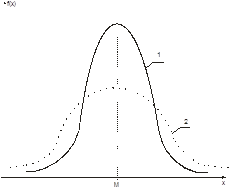
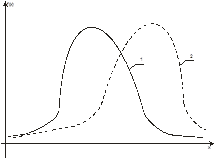
Рис 4.1. Кривые распределения 1- с положительным эксцессом, 2- с отрицательным эксцессом

Рис 4.2. Кривые распределения 1- с положительной асимметрией, 2- с отрицательной асимметрией

В работах В.А. Геодакяна (1974;1993)        исследовались распределения фенотипических признаков у мужчин и женщин. Фенотипическое распределение женского пола – это описанное выше первое распределение, а мужского – второе распределение. Мужчины – это передовая часть популяции, которая отвечает за поиск новых форм приспособления, поэтому у них чаще встречаются редкие крайние значения фенотипических признаков. По мнению В.А. Геодакяна эти отклонения от средних значений носят «футуристический» характер, это “пробы”, в которых содержатся как будущие возможные пути эволюции, так и ошибки на этом пути. В то же время, женская часть популяции ответственна за сохранение уже накопленных изменений, поэтому у нее чаще встречаются средние значения фенотипических признаков.

  Пример 2. Рассмотрим два распределения (рис.4.2), отличающихся по знаку асимметрии. Пусть первое распределение имеет положительную (левостороннюю) асимметрию, а второе – отрицательную (правостороннюю) асимметрию. В качестве иллюстрации такого вида распределений в психологии приведем следующий пример: испытуемым предлагается решить простую и сложную задачи, время решения задач каждым испытуемым фиксируется. Распределение с положительной асимметрией отражает распределение времени решения простой задачи: большинство испытуемых ее решают быстро, поэтому большая часть значений группируется слева. В то же время найдутся испытуемые, кто на решение простой задачи может потратить даже больше времени, чем на решение сложной (нет ли подвоха?). Трудную задачу большинство испытуемых решают дольше, чем простую (отрицательная асимметрия), хотя часто находятся люди, которые решают ее очень быстро.

  Если мы докажем, что рассмотренные распределения статистически достоверно различаются, то это может стать отправной точкой для дальнейших исследований. Например, можем выявить группу испытуемых со стандартным соотношением признаков: простую задачу решают быстро, а трудную – медленно, и группу испытуемых с нестандартным соотношением: простую задачу решают медленно, а трудную – быстро. Затем можем сравнить эти группы по другим показателям, скажем, по мотивации достижения результата. Известно, что люди с преобладанием стремления к успеху предпочитают задачи средней трудности, а люди с преобладанием стремления избегать неудачи предпочитают либо очень легкие, либо, наоборот, очень трудные задачи.

  Следует заметить, что кроме рассмотренных примеров в задачах психологии важное значение имеют сопоставления полученных в результате эксперимента эмпирических распределений с каким – либо теоретическим распределением (чаще всего с нормальным или равномерным законом). Для определения расхождения или согласия распределений обычно используются критерий c² Пирсона и критерий l Колмогорова – Смирнова.

  3. Критерий c² Пирсона.

       Области применения этого критерия многообразны; мы ограничимся двумя, наиболее часто встречающимися на практике применениями. Первая – это сопоставление эмпирического распределенияпризнака с теоретическим (нормальным, равномерным или иным). Вторая цель – сопоставление двух, трех или более эмпирических распределений одного и того же признака.

Критерий c² Пирсона отвечает на вопрос, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределении или в двух и более эмпирических распределениях.

Большим преимуществом этого метода является то, что он применим для сопоставления распределений признаков, представленных в любой шкале, даже в шкале наименований.

Если признак измеряется количественно и данных очень много, приходится объединять данные в несколько разрядов, как это принято в математической статистике. После этого сопоставляются частоты разрядов признака.

При сопоставлении эмпирического и теоретического распределений признака находится степень расхождения между эмпирическими и теоретическими частотами признака. При сопоставлении двух эмпирических распределений определяется степень расхождения между эмпирическими частотами и теоретическими частотами, которые наблюдались бы в случае совпадения этих двух распределений. Формулы расчета теоретических частот будут даны ниже для каждого из этих вариантов сопоставления. Расчет критерия Пирсона удобно производить по алгоритму 11, который приведем ниже.

В зависимости от поставленной задачи возможны несколько вариантов статистических гипотез.

Первый вариант гипотез:

Н₀: Полученное эмпирическое распределение признака не отличается от теоретического распределения.

Н₁: Полученное эмпирическое распределение признака отличается от теоретического распределения.

Второй вариант гипотез:

Н₀: Эмпирическое распределение 1 не отличается от эмпирического распределения 2.

Н₁: Эмпирическое распределение 1 отличается от эмпирического распределения 2.

Третий вариант гипотез:                        

Н₀: Эмпирические распределения 1, 2, 3, … не различаются между собой.

Н₁: Эмпирические распределения 1, 2, 3, … различаются между собой.

  Критерий c² позволяет проверить все три варианта гипотез. Чем больше расхождение между двумя сопоставляемыми распределениями, тем больше эмпирическое значение c².

  Для этого критерия существуют следующие ограничения.

1. Объем выборки n должен быть достаточно большим: n ³30.

2. Для каждого разряда таблицы теоретическая частота f должна быть не меньше 5: f ³5. Если k – количество разрядов задано заранее, то минимальное число наблюдений определяется по формуле: n_min= k×5.

3. Выбранные разряды должны включать в себя весь диапазон значений выборки, при этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях.

4. При сопоставлении распределений признаков, которые принимают только два значения, необходимо вносить «поправку на непрерывность».

  Особый случай №1: поправка на непрерывность.

  Эта поправка применяется в случаях:

а) если эмпирическое распределение сравнивается с равномерным, количество разрядов к = 2, то число степеней свободы n=к-1=1, и, фактически, проверяется, поровну ли распределились частоты между двумя значениями признака;

б) если сравниваются два эмпирических распределения (с=2), и количество разрядов признака к = 2, то опять n=(к-1)×(с-1) = 1.

  Сама поправка состоит в том, что при расчете критерия c² вместо разности f_эмп – f_теор берется разность ½f_эмп – f_теор ½– 0,5.

Особый случай №2: укрупнение разрядов признака.

Если значений признака очень много, то, очевидно, нельзя принимать каждое значение за самостоятельный разряд. Об этом, кстати, сказано в ограничении 2. Укрупнение разрядов производится в зависимости от диапазона значений, как это обычно делается в математической статистике. При этом надо обращать внимание на то, чтобы не терялась важная информация.

АЛГОРИТМ 11

Расчет критерия c² Пирсона.

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

3. Вычислить разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле n = к-1, где к – количество разрядов признака. Если n =1, внести поправку на непрерывность, заменив f _эмп – f _теор на ½f _эмп – f _теор ½ – 0,5.

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую частоту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как c² _эмп.

8. Определить по таблице критическое значение c² _кр для вычисленного n. Если c² _эмп< c² _кр, то расхождения между распределениями статистически недостоверны. Если c² _{эмп ³} c² _кр, то расхождения между распределениями статистически достоверны.