Нормальное распределение
Непрерывная случайная величина 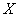 , распределённая по нормальному закону, имеет функцию плотности
, распределённая по нормальному закону, имеет функцию плотности 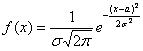 и однозначно определяется параметрами
и однозначно определяется параметрами 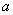 и
и 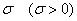 .
.

 (*)
(*)
В этой формуле  ,
, 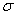 фиксированные параметры,
фиксированные параметры,  = m – среднее, математическое ожидание,
= m – среднее, математическое ожидание, 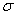 – стандартное отклонение, среднее квадратическое отклонение.
– стандартное отклонение, среднее квадратическое отклонение.
Начнём с того, что для функции 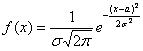 выполнены свойства плотности вероятностей, а именно
выполнены свойства плотности вероятностей, а именно  (почему?) и
(почему?) и  , откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.
, откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.
Любопытно отметить, что сам по себе неопределённый интеграл  является неберущимся, однако указанный выше несобственный интеграл сходится и равен
является неберущимся, однако указанный выше несобственный интеграл сходится и равен  . Вычисления для простейшего случая
. Вычисления для простейшего случая  можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены
можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены 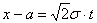 .
.
Следующие замечательные факты я тоже приведу без доказательства:
 – то есть, математическое ожидание нормально Xраспределённой случайной величины в точности равно «а», а среднее квадратическое отклонение в точности равно «сигме»:
– то есть, математическое ожидание нормально Xраспределённой случайной величины в точности равно «а», а среднее квадратическое отклонение в точности равно «сигме»:  .
.
Эти значения выводятся с помощью общих формулматематического ожиданияидисперсии, и желающие / нуждающиеся могут ознакомиться с подробными выкладками в учебной литературе, и совсем здОрово, если вам удастся провести их самостоятельно.
 .
.
Графики одномерного нормального распределения

Рисунок 1. График плотности нормального распределения: среднее равно 0, стандартное отклонение 1
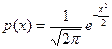
Свойства плотности.
1. 
2. 
Домашнее задание
1. Доказать  .
.
 . Следовательно, свойства плотности выполняются.
. Следовательно, свойства плотности выполняются.

Графики плотности при различных параметрах приведены ниже.
Рисунок 2. График плотности стандартного нормального распределения с областями, содержащими 68% и 95% всех наблюдений

Рисунок 3. Графики плотностей нормальных распределений c нулевым средним и разными отклонениями (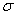 =0.5,
=0.5, 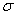 =1,
=1, 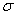 =2)
=2)

Кривая плотности нормального распределения симметрична относительно  и имеет в этой точке единственный максимум, равный
и имеет в этой точке единственный максимум, равный 
Параметр стандартного отклонения 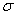 меняется в пределах от 0 до ∞.
меняется в пределах от 0 до ∞.
Среднее  меняется в пределах от -∞ до +∞.
меняется в пределах от -∞ до +∞.
При увеличении параметра 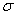 кривая растекается вдоль оси х, при стремлении
кривая растекается вдоль оси х, при стремлении 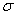 к 0 сжимается вокруг среднего значения (параметр
к 0 сжимается вокруг среднего значения (параметр 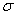 характеризует разброс, рассеяние).
характеризует разброс, рассеяние).
При изменении  кривая сдвигается вдоль оси х (см. графики).
кривая сдвигается вдоль оси х (см. графики).
Двумерное нормальное распределение
Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.
Общая формула для двумерного нормального распределения имеет вид:


Где  – парная корреляция между X1 и X2;
– парная корреляция между X1 и X2;
 – среднее и стандартное отклонение переменной X1 соответственно;
– среднее и стандартное отклонение переменной X1 соответственно;
 – среднее и стандартное отклонение переменной X2 соответственно.
– среднее и стандартное отклонение переменной X2 соответственно.
Если случайные величины Х1 и Х2 независимы, то корреляция равна 0,  = 0, соответственно средний член в экспоненте зануляется, и мы имеем:
= 0, соответственно средний член в экспоненте зануляется, и мы имеем:
f(x1,x2) = f(x1)*f(x2)
Для независимых величин двумерная плотность распадается в произведение двух одномерных плотностей.
 2020-06-08
2020-06-08 142
142







