Порядка с постоянными коэффициентами

Уравнение вида

где  - постоянные (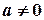), называется дифференциальным уравнением второго порядка с постоянными коэффициентами.

Если , то уравнение называется линейным однородным дифференциальным уравнением с постоянными коэффициентами, или уравнением без правой части: 

.

Последнее уравнение можно привести к виду

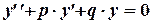
Уравнение

называется его характеристическим уравнением.

В зависимости от корней  и  характеристического уравнения получаем общее решение уравнения  в виде:

1.

если корни действительны и различны;

2.

если корни действительны и равны;

3.

если   - комплексные числа.

Пример. Проинтегрировать дифференциальное уравнение ; найти его частное решение, удовлетворяющее условиям:  .

Характеристическое уравнение будет иметь вид:

,

его корни равны

Общее решение будет иметь вид:

.

Чтобы найти указанное частное решение, подставим начальные данные. Для этого вначале найдем . В результате будем иметь систему:

Решив систему, найдем: . Отсюда