Построение сечений
(сечение на модели куба,
Методы построения сечений многогранников)
Проектная работа по математике
Выполнила ученица 10 класса «Б»
Захлебина Екатерина Дмитриевна
Научный руководитель:
учитель математики
Фурсова Ольга Ивановна
Тамбов
2019
Оглавление
1. Введение. 2
2. Цели и задачи, актуальность. 4
3. Основные этапы построения сечений куба. 5
4. Основная теория. 15
4.1. Построение сечений многогранников на основании системы аксиом и следствий из них. 15
4.2. Метод следов. 24
4.3. Метод внутреннего проектирования. 32
4.4. Комбинированный метод. 34
5. Заключение. 37
СПИСОК ЛИТЕРАТУРЫ.. 38
Введение
Материал по геометрии в 10 классе требует от человека пространственного восприятия мира. Пространственное мышление играет важную роль в познании человеком окружающей действительности, в овладении им различными профессиями. Решение пространственных задач осложняется тем, что в отличии от задач на построение на плоскости невозможно соединение формально-логической схемы построений с их действительным выполнением при помощи чертежных инструментов, то есть чертежные операции в пространстве не возможны. Поэтому пространственные задачи переносятся на проекционный чертеж и решаются на нем.
Наиболее эффективными средствами развития пространственных представлений учащихся, как известно, являются: демонстрация фигур, сравнение положений геометрических фигур относительно друг друга, моделирование, грамотное изображение фигур, чтение чертежа. Эти средства приводят к наилучшим результатам, если они используются систематически и в комплексе. Удобно, например, это проделать на изображении куба и правильного тетраэдра, сопровождая построения на изображении демонстрацией соответствующих отношений на модели. Все это будет способствовать укреплению связи изображения трёхмерного объекта и оригинала.
В своём проекте я решила создать макеты различных сечений куба, которые можно использовать на уроках, а так же глубже изучить методы построения сечений, подобрать задачи соответственно методу построения, разобрать их решение, и предложить ознакомить учащихся с данным материалом.
Цели и задачи, актуальность
Цель:
создание наглядных сечений на модели куба.
Задачи:
· изучить методы построения сечений многогранников;
· выполнить модели сечений на примере куба;
· подобрать необходимые задачи;
· провести урок для учащихся 10-х классов;
· подвести итоги.
Актуальность данного проекта заключается в том, что, несмотря на то, что тема «Построение сечений многогранников» изучается в школьной программе 10 класса, но у многих учеников возникают трудности при построении сечений многогранников из-за отсутствия наглядного представления. Однако необходимость выпускников школы в умении решать задачи на построение сечений многогранников очень большая. Это связано с тем, что на вступительных экзаменах в технические вузы все чаще встречаются задачи, в которых на каком-либо этапе решения необходимо построить сечение многогранника. Поэтому я решила глубже изучить методы построения сечений, а так же создать макеты различных сечений куба, которые были использованы мной и учителем на уроках, при прохождении материала. Данные модели можно использовать для развития интереса к предмету «геометрия».
Основные этапы построения сечений куба.
Мною были построены 4 модели сечений куба:
· сечением куба является треугольник,
· сечением куба является четырёхугольник,
· сечением куба является пятиугольник,
· сечением куба является шестиугольник.
Чтобы выполнить данные модели, мне необходимо было изучить теорию, произвести определённые расчёты при построении макета, т.е. решить задачи с разными условиями.
Задача 1. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через вершины А, В1, D1, если ребро куба равно 10см.
Решение: Т. к. точки А и В1 лежат в одной плоскости (АА1В1), то проведём АВ1. Точки В1 и D1 лежат в одной плоскости (А1В1D1), проведём В1D1. Точки А и D1 лежат в одной плоскости (АА1D1), проведём АD1. Искомым сечением является треугольник АВ1D1. Так как все грани куба равные квадраты со стороной 10 см (по условию), то АВ1D1 – равносторонний треугольник, сторона которого равна длине диагонали куба, т.е.  см.
см.







Задача 2. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через вершины А, В1, С1, если ребро куба равно 10см.
Решение. Т. к. точки А и В1 лежат в одной плоскости (АА1В1), то проведём АВ1. Рёбра куба AD и В1С1 параллельны, т.о. AD и В1С1 лежат в плоскости сечения. Точки D и С1 лежат в одной плоскости (DD1C1), проведём DС1. Искомым сечением является прямоугольник АВ1С1D. Так как все грани куба равные квадраты со стороной 10 см (по условию), то АВ1С1D – прямоугольник, стороны которого равны 10см и  см.
см.



Задача 3. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки В1, Р, К, если ребро куба равно 8см. Где В1 – вершина куба, Р 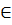 АА1 и А1Р=6см, К
АА1 и А1Р=6см, К 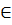 СС1 и С1К=6см.
СС1 и С1К=6см.

Проведём В1К, т.к. точки В1 и K лежат в одной плоскости (ВВ1С1). Проведём В1P, т.к. точки В1 и P лежат в одной плоскости (АА1В1).  ,
,
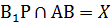 .
.  (по двум катетам), следовательно В1Р=В1К=10см (по теореме Пифагора).
(по двум катетам), следовательно В1Р=В1К=10см (по теореме Пифагора).  (по двум углам), следовательно
(по двум углам), следовательно  .
.  , т.е. CY=
, т.е. CY=  , KY=
, KY=  . Аналогично можно найти PX и AX, PX=KY=
. Аналогично можно найти PX и AX, PX=KY=  , AX=CY=
, AX=CY=  . B1X=B1P+PX=10см +
. B1X=B1P+PX=10см +  =
=  . B1Y=B1X=
. B1Y=B1X=  .
.

Проведём XY, т.к. точки X и Y лежат в одной плоскости (АВС).
 ,
,  .
.

Проведём KL, т.к. точки K и L лежат в одной плоскости (DCC1). Проведём PM, т.к. точки P и M лежат в одной плоскости (ADD1). Искомым сечением является пятиугольник B1KLMP. Т.к. секущая плоскость пересекает параллельные плоскости по параллельным прямым, то  ,
,  .
.

Т.к.  , то
, то  (прямая, параллельная стороне треугольника, отсекает от треугольника подобный ему треугольник). Значит,
(прямая, параллельная стороне треугольника, отсекает от треугольника подобный ему треугольник). Значит,  .
.  . Т.о. KL=
. Т.о. KL=  , аналогично PM=
, аналогично PM=  .
.  прямоугольный, используя теорему Пифагора, получаем, что CL=
прямоугольный, используя теорему Пифагора, получаем, что CL=  . Аналогично АМ=
. Аналогично АМ=  . DL=DM=8см -
. DL=DM=8см -  =
=  .
.  – прямоугольный, используя теорему Пифагора, получаем, что
– прямоугольный, используя теорему Пифагора, получаем, что  см.
см.

Задача 4. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки М, Р, К, если ребро куба равно 10см. Где М – середина ребра A1B1, Р – середина ребра B1C1, К – середина ребра СD.
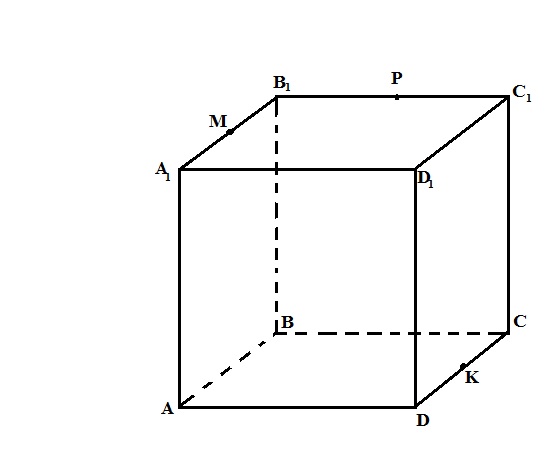
Проведём МР, т.к. точки М и Р лежат в одной плоскости (А1В1С1). Плоскости (АВС) и (А1В1С1) параллельны, значит секущая плоскость пересекает их по параллельным прямым. Проведём  , где
, где 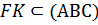 . Т.к. М и Р – середины рёбер куба A1B1 и В1С1, то B1М= B1Р=5см.
. Т.к. М и Р – середины рёбер куба A1B1 и В1С1, то B1М= B1Р=5см.  – прямоугольный. Используя теорему Пифагора, получаем, что МР=
– прямоугольный. Используя теорему Пифагора, получаем, что МР=  см. Т.к.
см. Т.к.  и К – середина CD, то FD=5см. Аналогично можно найти FK, FK=
и К – середина CD, то FD=5см. Аналогично можно найти FK, FK=  см
см
 ,
,  . Т.к. К – середина CD,
. Т.к. К – середина CD,  (как вертикальные),
(как вертикальные),  , то
, то  (по катету и прилежащему острому углу). Значит, CY=DF=5см. Аналогично можно найти AX, AX=5см.
(по катету и прилежащему острому углу). Значит, CY=DF=5см. Аналогично можно найти AX, AX=5см.

Проведём МX, т.к. точки М и X лежат в одной плоскости (АА1В1).
 . Проведём PY, т.к. точки P и Y лежат в одной плоскости (BB1C1).
. Проведём PY, т.к. точки P и Y лежат в одной плоскости (BB1C1). 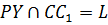 .
.  ,
,  (по катету и противолежащему острому углу). Следовательно, MN=NX=
(по катету и противолежащему острому углу). Следовательно, MN=NX=  см, PL=LY=
см, PL=LY=  см.
см.
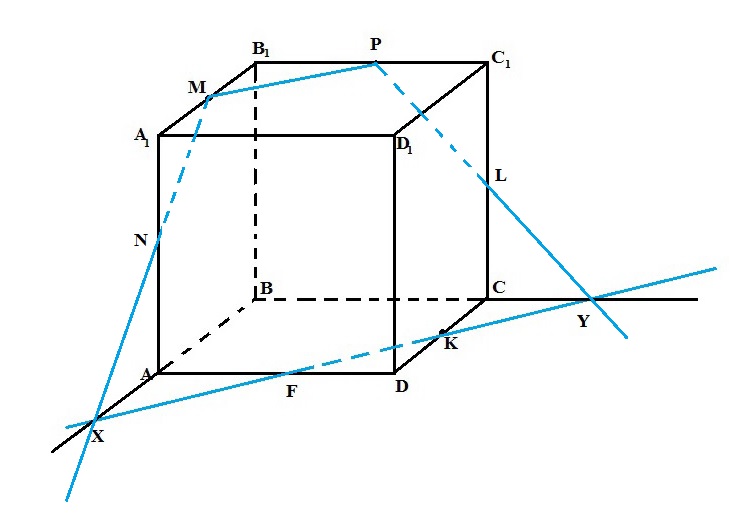
Проведём KL, т.к. точки K и L лежат в одной плоскости (CC1D1). Проведём NF, т.к. точки N и F лежат в одной плоскости (АА1D1). Аналогично можно найти KL и NF, KL=NF=  см. Искомым сечением является правильный шестиугольник MPLKFN, сторона которого равна 5
см. Искомым сечением является правильный шестиугольник MPLKFN, сторона которого равна 5 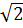 см.
см.


Основная теория
 2020-06-08
2020-06-08 992
992







