Определение. Сечением многогранника плоскостью называется геометрическая фигура, представляющая собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости; плоскость при этом называется секущей плоскостью.
Поверхность многогранника состоит из ребер - отрезков и граней - плоских многоугольников. Так как прямая и плоскость пересекаются в точке, а две плоскости - по прямой, то сечением многогранника плоскостью является плоский многоугольник; вершинами этого многоугольника служат точки пересечения секущей плоскости с ребрами многогранника, а сторонами - отрезки, по которым секущая плоскость пересекает его грани. Это означает, что для построения искомого сечения данного многогранника плоскостью αдостаточно построить точки ее пересечения с ребрами многогранника. Затем последовательно соединить отрезками эти точки.
Секущая плоскость α может быть задана: тремя точками, не лежащими на одной прямой; прямой и не принадлежащей ей точкой; двумя пересекающимися прямыми; двумя параллельными прямыми; другими условиями, определяющими ее положение относительно данного многогранника.Сечения многогранников используются при решении многих задач стереометрии. При этом стоит отметить, что, говоря о построениях в пространстве, обычно имеют в виду не столько реальные построения, сколько утверждении о существовании объектов. Например, фраза "проведем плоскость через течки А, В, С" означает ''фиксируем, что существует плоскость, проходящая через точки А, В, С". Аналогичный смысл имеет "проведение" прямых в пространстве. При таком подходе построение фигуры в пространстве (сечения, в частности) фактически означает доказательство ее существования, основанное на аксиомах.
Построения сечений многогранников также можно производить, основываясь на следующих следствиях аксиом стереометрии:
1. Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является прямой пересечения данных плоскостей.
2. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны.
3. Для построения сечений, перпендикулярных прямой или плоскости, используются теоремы о перпендикулярности прямых и плоскостей.
Задачи на сечения многогранников.
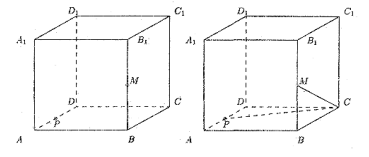
Задача 1. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через ребро АА1 и точку М ребра CD.
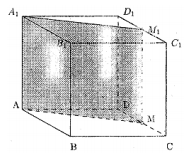
Решение.
Через точку М и прямую АА1 можно провести плоскость (обозначим ее а) и притом только одну. Найдем, как эта плоскость пересекается с гранями и ребрами параллелепипеда.
1) Так как точки А и М являются общими для плоскостей а и ABCD, то прямая AM является прямой пересечения этих плоскостей. Соединим точки А и М отрезком.
2) Так как плоскости АВВ1А1 и DCC1D1 параллельны, то секущая плоскость и пересекает их по параллельным прямым. Через точку М параллельно ребру СС1 проведем прямую ММ1 (М1 — точка пересечения с ребром C1D1).
3) Так как точки А1 и М1 являются общими для плоскостей а и A1B1C1D1, то прямая А1М1 является прямой пересечении этих плоскостей. Соединим точки А1 и М1. Искомое сечение четырехугольник AMM1А1.
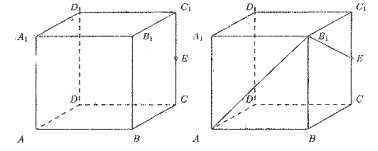
Задача 2. ABCDA1B1C1D1 — куб, E — середина СС1. Определите число сторон сечения плоскостью, которая проходит через точки A, B1, E.
Решение.
Обозначим через 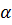 плоскость, содержащую искомое сечение. Очевидно, что
плоскость, содержащую искомое сечение. Очевидно, что 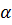 пересекается с гранями AA1B1B и ВВ1С1С по прямым AB1 и В1Е соответственно. Грани AA1B1B и DD1С1С куба параллельны, поэтому прямые, по которым плоскость
пересекается с гранями AA1B1B и ВВ1С1С по прямым AB1 и В1Е соответственно. Грани AA1B1B и DD1С1С куба параллельны, поэтому прямые, по которым плоскость 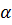 пересекается с ними, также будут параллельны. Одна из этих прямых — АВ1. Построить параллельную ей прямую в плоскости DD1С1С можно следующим образом: через точку Е проведем прямую, параллельную диагонали С1D. Точка пересечения К этой прямой с ребром DC делит его пополам (теорема Фалеса).
пересекается с ними, также будут параллельны. Одна из этих прямых — АВ1. Построить параллельную ей прямую в плоскости DD1С1С можно следующим образом: через точку Е проведем прямую, параллельную диагонали С1D. Точка пересечения К этой прямой с ребром DC делит его пополам (теорема Фалеса).
Итак, для построения линии пересечения плоскости 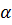 и грани DD1С1С делим отрезок DC пополам и соединяем точки К и Е.
и грани DD1С1С делим отрезок DC пополам и соединяем точки К и Е.
Так как точки А и К являются общими для плоскостей а и ABCD, то прямая АК является прямой пересечения этих плоскостей. Соединим точки А и К. Искомое сечение — четырехугольник АВ1ЕК.
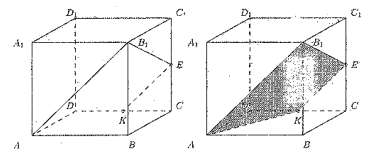
Задача 3. ABCDA1B1C1D1— куб. К — середина AD. M — середина CD. В каком отношении, считая от точки А, делит ребро АA1 плоскость, проходящая через точки В1, К и М?
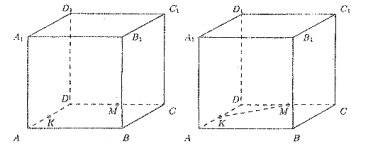
Решение.
Обозначим через 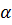 плоскость, проходящую через точки К, М и В1. Построим сечение куба этой плоскости. Точки К и М являются общими для плоскости
плоскость, проходящую через точки К, М и В1. Построим сечение куба этой плоскости. Точки К и М являются общими для плоскости 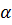 и плоскости ABCD, поэтому прямая КМ является прямой пересечения этих плоскостей. Продолжим прямую КМ до пересечения с ребрами АВ и ВС. Пусть
и плоскости ABCD, поэтому прямая КМ является прямой пересечения этих плоскостей. Продолжим прямую КМ до пересечения с ребрами АВ и ВС. Пусть 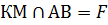 ,
, 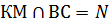 .
.
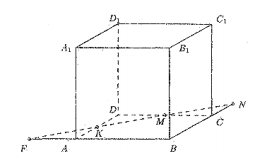
Точки В1 и N являются общими для плоскостей 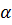 и ВВ1С1С, поэтому прямая B1N — это линия пересечения этих плоскостей. Обозначим S —точку пересечения прямых B1N и С1С.
и ВВ1С1С, поэтому прямая B1N — это линия пересечения этих плоскостей. Обозначим S —точку пересечения прямых B1N и С1С.
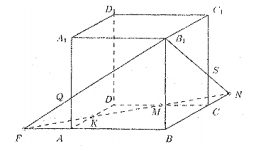
Аналогично строится точка Q (пересечение B1F и AA1). Точки S и М являются общими для плоскостей 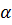 и DD1С1С, поэтому прямая SM — это прямая пересечения этих плоскостей. Точки Q и K являются общими для плоскостей
и DD1С1С, поэтому прямая SM — это прямая пересечения этих плоскостей. Точки Q и K являются общими для плоскостей 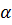 и DD1А1А, поэтому прямая QK — это прямая пересечения этих плоскостей. Искомое сечение — пятиугольник B1SMKQ.
и DD1А1А, поэтому прямая QK — это прямая пересечения этих плоскостей. Искомое сечение — пятиугольник B1SMKQ.
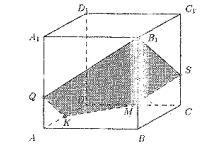
Найдём отношение AQ: QA1. Из построения ясно, что ΔFKA равен треугольнику КDМ, следовательно, AF = 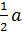 , где a — ребро куба. Из подобия треугольников AQF и A1QB1 находим AQ: QA1 = 1: 2.
, где a — ребро куба. Из подобия треугольников AQF и A1QB1 находим AQ: QA1 = 1: 2.
Ответ: AQ: QA1 = 1:2
Задача 4. ABCDA1B1C1D1 — куб. Найдите угол между АВ1 и ВС1.
Решение.
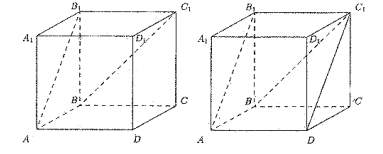
Через прямую ВС1 проведем плоскость, параллельную прямой АВ1, точнее говоря, построим сечение куба этой плоскостью. Обозначим 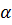 — искомую плоскость. Диагональ C1D грани DD1С1С параллельна диагонали В1А, противоположной грани куба, а так как точка С1 принадлежит
— искомую плоскость. Диагональ C1D грани DD1С1С параллельна диагонали В1А, противоположной грани куба, а так как точка С1 принадлежит 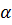 , то и вся прямая C1D принадлежит
, то и вся прямая C1D принадлежит 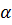 , следовательно, она является линией пересечения плоскости
, следовательно, она является линией пересечения плоскости 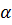 с гранью DD1С1С. Так как точки В и D являются общими для плоскостей
с гранью DD1С1С. Так как точки В и D являются общими для плоскостей 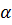 и ABCD, то эти плоскости пересекаются по прямой BD. Искомое сечение — это треугольник BC1D.
и ABCD, то эти плоскости пересекаются по прямой BD. Искомое сечение — это треугольник BC1D.
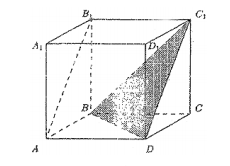
Угол между скрещивающимися прямыми АВ1 и ВС1 равен углу DC1B, так как прямые AB1 и DC1 параллельны. Треугольник BC1D – равносторонний, поэтому искомый угол равен 60°.
Ответ: 60°.
Задача 5. Основание прямоугольного параллелепипеда ABCDA1B1C1D1 — квадрат со стороной 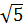 см, длина ребра AA1 = 2
см, длина ребра AA1 = 2 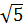 см. Найдите площадь сечения, проведенного через точки С, Р и M, где Р — середина AD и М — середина ВВ1.
см. Найдите площадь сечения, проведенного через точки С, Р и M, где Р — середина AD и М — середина ВВ1.
Решение.
Построим искомое сечение параллелепипеда. Пусть 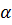 — плоскость, в которой лежит это сечение. Очевидным образом прямые МС и СР являются прямыми, по которым плоскость а пересекается с гранями ВВ1С1С и АBCD соответственно. Продолжим прямые PC и АВ и обозначим Q — точку их пересечения.
— плоскость, в которой лежит это сечение. Очевидным образом прямые МС и СР являются прямыми, по которым плоскость а пересекается с гранями ВВ1С1С и АBCD соответственно. Продолжим прямые PC и АВ и обозначим Q — точку их пересечения.
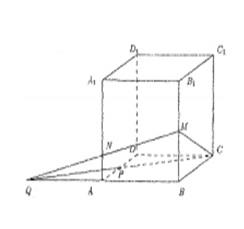
Точки Q и М являются общими для плоскости 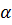 и плоскости АВВ1А1, поэтому прямая QM является прямой, по которой эти плоскости пересекаются. Обозначим N — точку пересечения прямых QM и AA1. Точки N и Р являются общими для плоскостей а и AA1D1D, поэтому их пересечением является прямая NP.
и плоскости АВВ1А1, поэтому прямая QM является прямой, по которой эти плоскости пересекаются. Обозначим N — точку пересечения прямых QM и AA1. Точки N и Р являются общими для плоскостей а и AA1D1D, поэтому их пересечением является прямая NP.
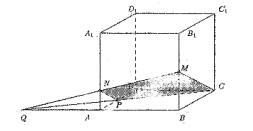
Искомое сечение — четырехугольник MNPC. Вычислим стороны этого четырехугольника.
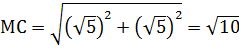 ,
,
РС = 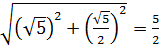 ,
,
PN = 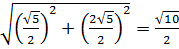 ,
,
MN = 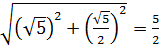 .
.
Таким образом, сечение — равнобокая трапеция.
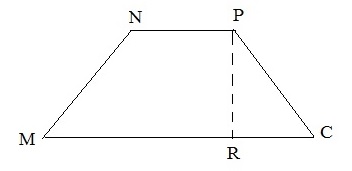
Ее высота равна PR = 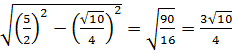 .
.
Искомая площадь сечения равна 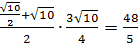 .
.
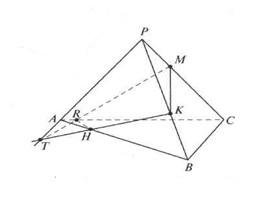
Задача 6. Постройте сечение тетраэдра РАВС плоскостью α = (МКH), где М, К и Н — внутренние точки соответственно ребер РС, РВ и АВ.
Решение.
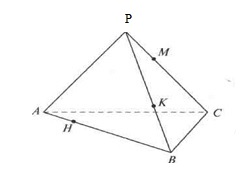
Точки М и K лежат в каждой из двух плоскостей α и (РВС). Поэтому по аксиоме пересечения двух плоскостей плоскость α пересекает плоскость (РВС) по прямой МК. Следовательно, отрезок МК — одна из сторон искомого сечения. Аналогично, отрезок КН — другая сторона искомого сечения.
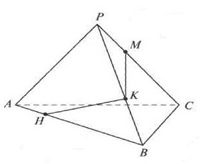
Точки М и Н не лежат одновременно ни в одной из граней пирамиды РАВС, поэтому отрезок МН не является стороной сечения этой пирамиды. Прямые КН и РА лежат в плоскости грани АВР и пересекаются. Построим точку T= КН ∩АР.
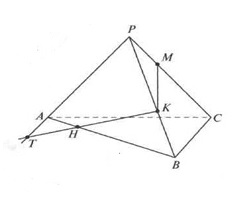
Т.к. прямая КН лежит в плоскости α, то и точка T лежит в плоскости α. Теперь мы видим, что плоскости αи (АРС) имеют общие точки М и T. Следовательно, по аксиоме пересечения двух плоскостей плоскость α и плоскость (АРС) пересекаются по прямой МТ, которая, в свою очередь, пересекает ребро АС в точке R.
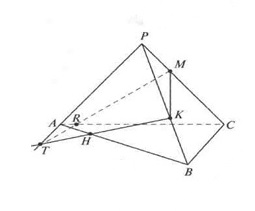
Плоскость α пересекает грани (АСР) и (АВС) по отрезкам MR и HR соответственно. Следовательно, искомое сечение — четырехугольник MKHR.
Метод следов
Существуют и другие методы построения плоских сечений многогранников. Наиболее эффективными являются метод следов, метод внутреннего проектирования и комбинированный метод.
Метод следов.
Определение. Прямая, по которой секущая плоскость 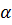 пересекает плоскость основания многогранника, называется следом плоскости
пересекает плоскость основания многогранника, называется следом плоскости 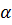 в плоскости этого основания.
в плоскости этого основания.
Из определения следа получаем: в каждой его точке пересекаются прямые, одна из которых лежит в секущей плоскости, другая – в плоскости основания. Именно это свойство следа используют при построении плоских сечений многогранников методом следов. Причём в секущей плоскости удобно использовать такие прямые, которые пересекают рёбра многогранника.
Способ следов состоит в следующем. Вначале строят на основной плоскости след секущей плоскости (причем за основную плоскость принимают большей частью плоскость основания геометрического тела). Затем, используя след секущей плоскости, находят точки встречи ребер многогранника с секущей плоскостью. Используя полученные (и данные) точки, получают следы секущей плоскости на гранях многогранника.
Рассмотрим решение задачи на построение сечения призмы плоскостью, используя ее след.
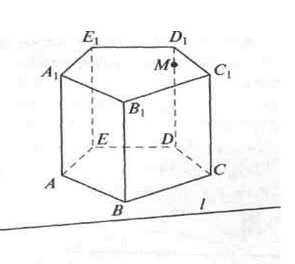
Задача 1. Построить сечение призмы АВСВЕА1В1С1D1Е1 плоскостью α, которая задана следом l в плоскости АВС основания призмы и точкой М, принадлежащей ребру DD1.
Решение.
Так как прямая l лежит в плоскости основания призмы, то она может пересекать плоскость грани СDD1C1 лишь в точке, которая принадлежит прямой CD = (CDD1) ∩ (АВС), т.е. точка X = l ∩ СD = l ∩ (CDD1) принадлежит секущей плоскости α. Таким образом, для построения точки N = α ∩ СС1 достаточно построить точку X = l ∩ СD.
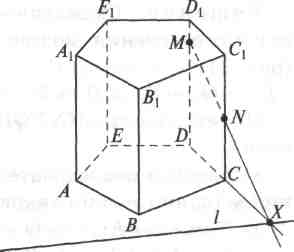
Аналогично, для построения точек Р = α ∩ ВВ1, Q = α ∩ АА1 и R = α ∩ ЕЕ1 достаточно построить соответственно точки: У = l ∩ ВС, Z = l ∩ АВ и Т = l ∩ АЕ.
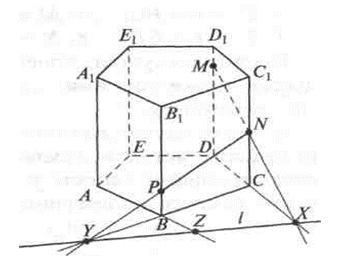
Отсюда построение.
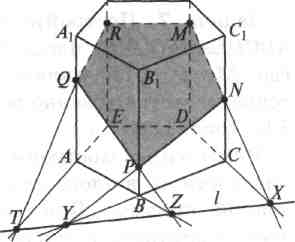
1. X = l ∩ СD;
2. N = МХ ∩ СС1;
3. У = l ∩ ВС;
4. Р = NY ∩ ВВ1;
5. Z = l ∩ АВ;
6. Q= РZ ∩ АА1;

7. T= l ∩ АЕ;
8. R= QT ∩ ЕЕ1.
9. Пятиугольник MNPQR — искомое сечение.
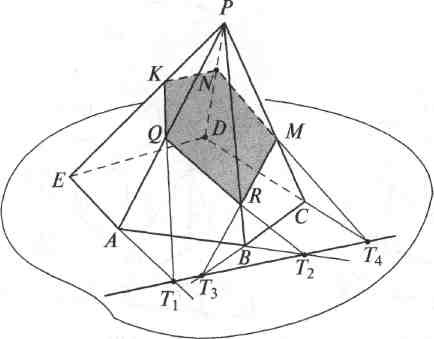
Задача 2. Построить сечение пятиугольной пирамиды PABCDE плоскостью, которая задана следом l и внутренней точкой К ребра РЕ.
Решение.
1. Т1= l ∩ АЕ; 2. Q = Т1К ∩ РА;
3. Т2 = l ∩ АВ; 4. R = Т2Q ∩ РВ;
5. Т3 = l ∩ ВС; 6. М = T3R ∩ РС;
7. Т4 = l ∩ СD; 8. N = Т4М ∩ РD;
9. KN;
10. KQRMN – искомое сечение.
Задача 3. АВСА1В1С1 – прямая треугольная призма. Постройте сечение призмы плоскостью (MPN), где M 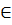 (ACC1), N
(ACC1), N 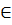 (BCC1), P
(BCC1), P 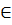 (ABB1). Причём МР и MN не параллельны плоскости основания.
(ABB1). Причём МР и MN не параллельны плоскости основания.
Решение.
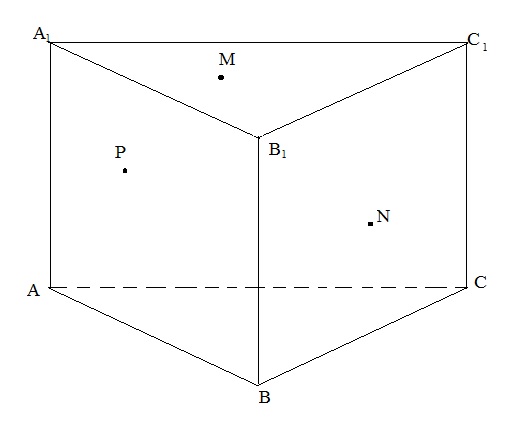
1. 
2. 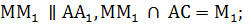
3. 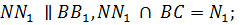
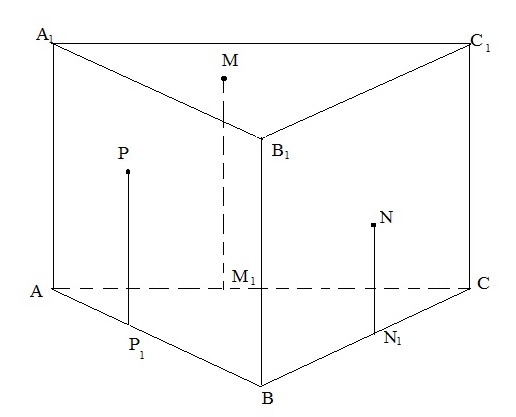
4. 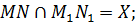
5. 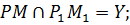
6. XY, XY  (ABC). XY – след секущей плоскости на плоскость (АВС);
(ABC). XY – след секущей плоскости на плоскость (АВС);
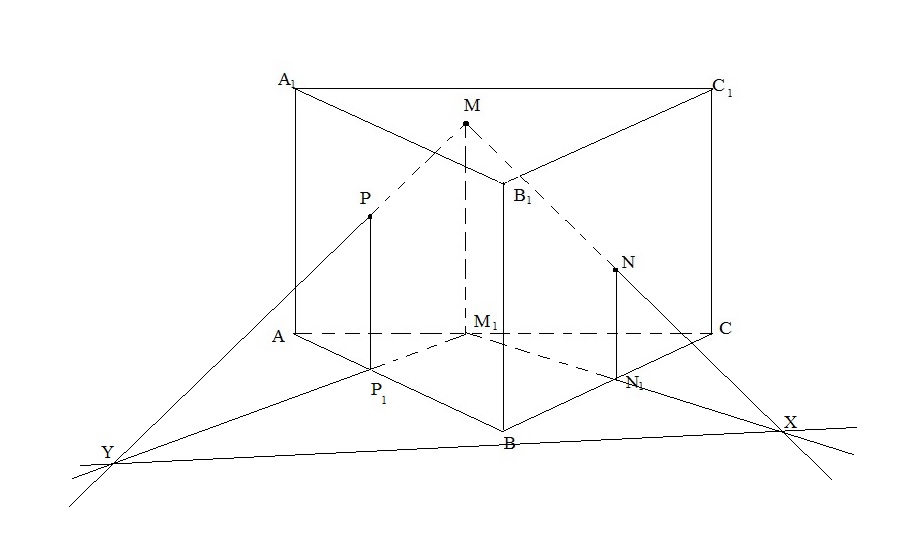
7. 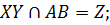
8. 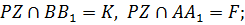
9. 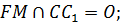
10. 
11. KFO – искомое сечение.
Задача 4. В кубе ABCDA1B1C1D1 со стороной 8 см точки Р, М, Т середины рёбер А1В1, СС1 и AD соответственно. Постройте сечение куба плоскостью, проходящей через точки Р, М, Т и найдите площадь этого сечения.
Решение.
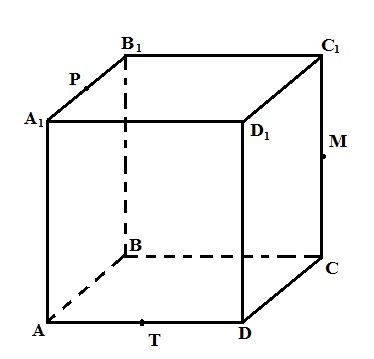
1. 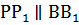 ;
;
2. 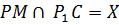 ;
;
3. 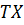 – след секущей плоскости на плоскость (АВС);
– след секущей плоскости на плоскость (АВС);
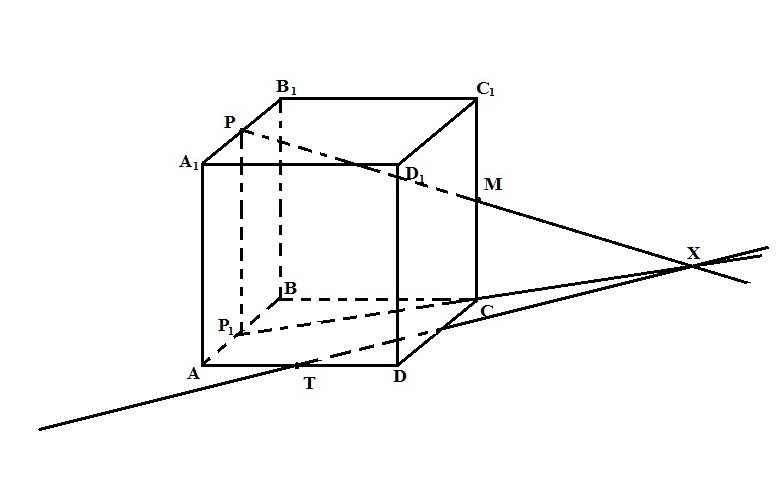
4. 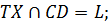
5. 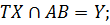
6. 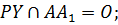
7. PO, TO, TL, LM;
8. 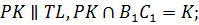
9. 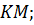
10. PKMLTO – искомое сечение.
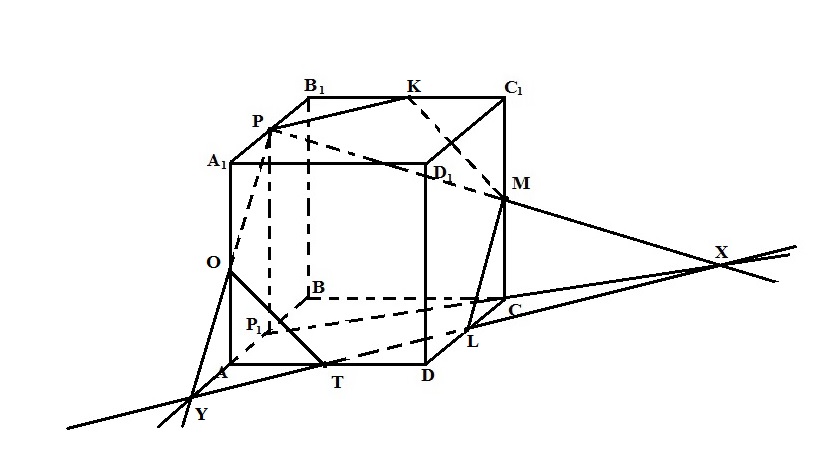
Можно доказать, что PKMLTO – правильный шестиугольник со стороной 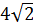 см, следовательно его площадь равна
см, следовательно его площадь равна 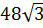 см2.
см2.
 2020-06-08
2020-06-08 929
929








