2020-06-08
587Для раскрытия неопределенностей используют следующее:
- упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, помножают на сопряженное, что позволяет в дальнейшем сократить и т.д.;
- если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: вычислим предел. 
Разложим числитель на множители 
Вычисление пределов функции
Пример 1. Вычислите предел функции:
Любой предел состоит из трех частей:
1) Всем известного значка предела lim.
2) Записи под значком предела, в данном случае 
.
Запись читается «икс стремится к единице». Чаще всего – именно x, хотя вместо «икса» на практике встречаются и другие переменные.
В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (∞).
3) Функции под знаком предела, в данном случае 
.
Сама запись читается так: «предел функции при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое.
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Пример 2. Вычислите предел функции: 
При прямой подстановке, получается неопределенность:
Разложим на множители числитель и знаменатель и вычислим предел.
Пример 2. Вычислите предел функции: 
Разбираемся, что такое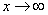 
? Это тот случай, когда 
неограниченно возрастает, то есть: сначала 
, потом 
, потом 
, затем 
и так далее до бесконечности.
А что в это время происходит с функцией 
?
, 
, 
, …
Итак: если 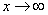, то функция стремится к минус бесконечности:
Т.е. согласно нашему первому правилу, мы вместо «икса» подставляем в функцию
бесконечность и получаем ответ.
Пример 3. Вычислите предел функции: 
Опять начинаем увеличивать до бесконечности и смотрим на поведение функции:
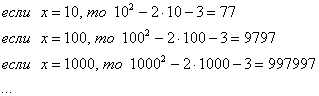
Вывод: при 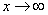функция 
неограниченно возрастает:
Закрепление материала (решение задач)
Вычислите пределы: 1)
Домашнее задание
Вычислите пределы функций
1) 
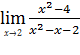
2) 
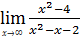
3) 
4) 
5) 
6) 
7) 
*
