Пример 1: Найти области сходимости степенных рядов:
а) 
б) 
в) 
Решение. а) Составим ряд из абсолютных величин членов данного ряда:
 .
.
Согласно признаку Даламбера полученный знакоположительный ряд сходится (абсолютно) при тех значениях х, для которых 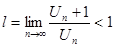 . Здесь
. Здесь  ,
,

 .Отсюда
.Отсюда

Определим, при каких значениях х этот предел l будет меньше единицы. Для этого решим неравенство  , или | x +1| < 2, откуда -3 < x < 1.Таким образом, первоначальный ряд сходится (абсолютно) в промежутке(-3, 1) - это и есть промежуток сходимости данного ряда.
, или | x +1| < 2, откуда -3 < x < 1.Таким образом, первоначальный ряд сходится (абсолютно) в промежутке(-3, 1) - это и есть промежуток сходимости данного ряда.
Исследуем сходимость ряда на концах промежутка сходимости. При
х = - 3 получаем числовой ряд
 .
.
Это – гармонический ряд, который, как известно, расходится.
При х= 1 получаем числовой знакочередующийся ряд
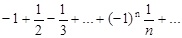 ,
,
который по признаку Лейбница сходится (условно).
Итак, область сходимости данного ряда – полуоткрытый промежуток 
б) Здесь  Отсюда
Отсюда

т.е. 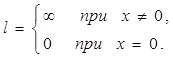
Таким образом, согласно признаку Даламбера ряд сходится только в точке
х = 0.
в) Имеем  Отсюда
Отсюда


Следовательно, при любом х по признаку Даламбера данный ряд абсолютно сходится. Область сходимости рассматриваемого ряда есть вся числовая ось.
Пример 2. разложите в ряд Тейлора по степеням х – 2 функцию 
Решение. Вычислим значения данной функции и ее последовательных производных при x=2:


……………………………….

………………………………….
Подставляя найденные значения и общее выражение ряда Тейлора для производной функции, получим

Это и есть разложение ряд Тейлора по степеням х – 2 для функции  Полученный ряд сходится к порождающей его функции
Полученный ряд сходится к порождающей его функции 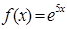 при любом значении х.
при любом значении х.
Заметим, что искомое разложение можно получить также следующим образом. В разложение (3) заменим х на 5х; тем самым получим ряд Маклорена для функции  . (*)
. (*)
Представив теперь функцию  в виде
в виде 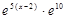 и подставляя в соотношение
и подставляя в соотношение
(*) х - 2 вместо х, приходим к разложению

Пример 3. разложить в ряд Маклорена функцию 
 Решение. Заменяя в разложении (8) х на – 2х, получим
Решение. Заменяя в разложении (8) х на – 2х, получим
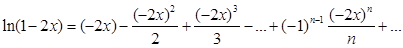 ,
,
или  .
.
Разложение (8) справедливо в промежутке 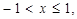 а искомое получается в результате замены х на – 2 х. Следовательно, для нахождения промежутка сходимости полученного ряда нужно решить неравенство
а искомое получается в результате замены х на – 2 х. Следовательно, для нахождения промежутка сходимости полученного ряда нужно решить неравенство 

Пример 4. Разложить в ряд Маклорена функцию 
Решение. По известной тригонометрической формуле имеем
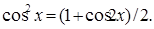
Разложить в ряд Маклорена функцию cos2x, заменяя в разложении (5) х на 2х:

или
 (*)
(*)
Разложение (5) справедливо при любом х, поэтому ряд Маклорена для cos 2x сходится к порождающей его функции также на всей числовой оси.
Для того чтобы получить разложение в ряд Маклорена функции  cos2x,
cos2x,
умножим все члены ряда (*) на ½:
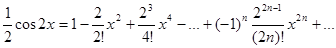 .
.
Тогда
 .
.
Это и есть разложение в ряд Маклорена функции  Очевидно, что оно справедливо при любом х.
Очевидно, что оно справедливо при любом х.
Пример 5. Приложение рядов к приближенным вычислениям.
Вычислить  , ограничиваясь первыми двумя членами ряда Маклорена для sin x, и оценить получающуюся при этом погрешность.
, ограничиваясь первыми двумя членами ряда Маклорена для sin x, и оценить получающуюся при этом погрешность.
Решение. Так как разложение (4) справедливо при любом х, то, в частности, при  имеем
имеем
 .
.
Полученный ряд - знакочередующийся. Ограничиваясь двумя членами этого ряда, т. е. считая  равным их сумме, мы тем самым допускаем ошибку, не превосходящую первого отбрасываемого члена
равным их сумме, мы тем самым допускаем ошибку, не превосходящую первого отбрасываемого члена  .Так как
.Так как  <0,0001, то с точностью до 0,0001 получаем
<0,0001, то с точностью до 0,0001 получаем
 .
.
Пример 6. Вычислить  с точностью до 0,01.
с точностью до 0,01.
Решение. Пользуясь разложением (3), при х=2 получим
 .
.
Остается решить вопрос о том, сколько членов данного ряда надо взять, чтобы получить значение  с требуемой точностью. Пусть искомое число членов равно
с требуемой точностью. Пусть искомое число членов равно  . Это означает, что ошибка
. Это означает, что ошибка  , которую мы допускаем, заменяя сумму ряда его
, которую мы допускаем, заменяя сумму ряда его  частичной суммой, равна сумме членов ряда, начиная с
частичной суммой, равна сумме членов ряда, начиная с  -го:
-го:
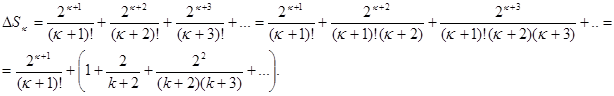
Если заменить каждое из чисел  числом
числом 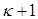 , то знаменатели дробей уменьшается, а сами дроби, следовательно, увеличиваются. Поэтому
, то знаменатели дробей уменьшается, а сами дроби, следовательно, увеличиваются. Поэтому

Выражение, стоящие в квадратной скобке, есть сумма членов бесконечно убывающей геометрической прогрессии со знаменателем  и следовательно, равно
и следовательно, равно

Таким образом,

Но, с другой стороны, ошибка  не должна превосходить 0,01:
не должна превосходить 0,01: 
Решая методом подбора неравенство

получим 
Итак, для достижения требуемой точности надо взять 8 членов ряда:

Пример 7. Вычислить  с точностью до 0.01.
с точностью до 0.01.
Решение. Данный определенный интеграл можно вычислить только приближенно.
Для этого разложим подынтегральную функцию вряд Тейлора:
 .
.
Отсюда
 здесь мы ограничились двумя первыми этого знакопеременного ряда,
здесь мы ограничились двумя первыми этого знакопеременного ряда,
так как третий член 1/(5!5) меньше 0,01.
Задания для практического занятия:
Вариант 1:
1.Найти область сходимости заданного степенного ряда.

2. Разложить в ряд Маклорена
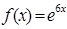
3. Вычислить  с точностью до 0.001.
с точностью до 0.001.
Вариант 2:
1.Найти область сходимости заданного степенного ряда
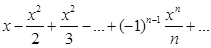
2. Разложить в ряд Маклорена

3. Вычислить  с точностью до 0.1.
с точностью до 0.1.
Вариант 3:
1.Найти область сходимости заданного степенного ряда

2.Разложить в ряд Маклорена

3. Вычислить  с точностью до 0.0001.
с точностью до 0.0001.
Вариант 4:
1.Найти область сходимости заданного степенного ряда

2.Разложить в ряд Маклорена

3.Вычислить  с точностью до 0.1.
с точностью до 0.1.
Контрольные вопросы
1.Какие ряды называются функциональными рядами?
2.Какой признак применяют при исследовании степенных рядов на сходимость?
 2020-06-08
2020-06-08 80
80







