Практическое занятие №17
Тема: «Разложение основных элементарных функций в ряд»
Цель: научиться исследовать степенные ряды на сходимость и раскладывать функции в ряд Маклорена
Краткие теоретические и учебно-методические материалы по теме практической работы
Ряды членами которого являются функции от x, называется функциональным. При одних значениях х ряд может сходиться, а при других – расходиться.


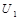 (x)+
(x)+ 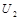 (x)+...+
(x)+...+ 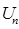 (X)+...=
(X)+...= 
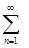
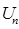 (x), (1)
(x), (1)
Функциональный ряд (1) называется сходящимся в точке 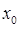 , если при
, если при 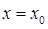 он обращается в сходящийся числовой ряд, если же при
он обращается в сходящийся числовой ряд, если же при 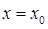 получается расходящийся числовой ряд, то ряд (1) называется расходящимся в точке
получается расходящийся числовой ряд, то ряд (1) называется расходящимся в точке 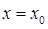 .
.
Совокупность значений х, при которых ряд (1) сходится, называется областью сходимости функционального ряда.
Из всех функциональных рядов наиболее распространенными на практике являются степенные ряды вида
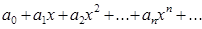 (2)
(2)
или более общего вида
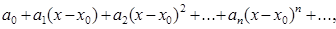 (3)
(3)
где постоянные 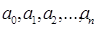 называется коэффициентами ряда.
называется коэффициентами ряда.
Областью сходимости любого степенного ряда вида (2) служит промежуток (– R; R) числовой оси, симметрично точке х=0, дополненный, быть может, его концами. Этот промежуток, называемый промежутком сходимости, обладает тем свойством, что при всех | x | < R ряд сходится, притом абсолютно, а при всех | x | > R – расходится. На концах промежутка сходимости, т. е. в точках х = - R и х = R, возможна как сходимость, так и расходимость степенного ряда.
Для нахождения области сходимости степенного ряда (2), применяется признак Даламбера к ряду, членами которого служат абсолютные величины членов рассматриваемого степенного ряда, а затем исследуется сходимость ряда на концах промежутка сходимости.
Разложение элементарных функций в степенные ряды
Рядом Тейлора для f(x) называются степенной ряд вида
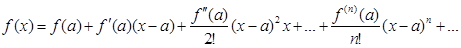 . (1)
. (1)
Если а = 0, то получается ряд
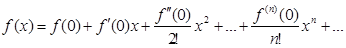 . (2)
. (2)
который называется рядом Маклорена.
При представлении элементарной функции в виде суммы ряда Тейлора обычно поступают следующим образом: вычисляют последовательные производные данной функции в точке х = а, а затем, пользуясь (1), составляют для нее ряд Тейлора и определяют промежуток сходимости полученного ряда. В этом промежутке ряд Тейлора сходится к порождающей его функции f(x), если только все значения 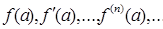 получается непосредственной подстановкой значения х = а в выражения
получается непосредственной подстановкой значения х = а в выражения 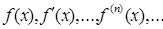 .
.
Применяя указанный способ, можно найти разложение в ряд Маклорена для следующих функций:
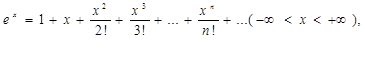 (3)
(3)
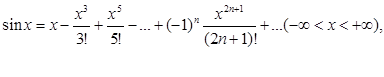 (4)
(4)
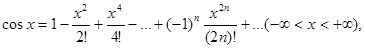 (5)
(5)
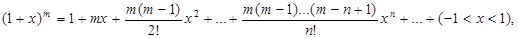 (6)
(6)
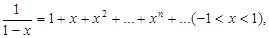 (7)
(7)
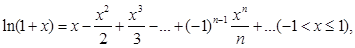 (8)
(8)
Помимо приведенного выше способа, можно получить разложения функций в ряд Тейлора, исходя из известных разложений, например, разложений
(3)-(8). При этом возможно использование следующих действий над степенными рядами внутри их промежутков сходимости:
1)два степенных ряда можно почленно складывать и умножать(по правилу умножения многочленов);
2)степенной ряд можно почленно умножать на общий множитель;
3)степенной ряд можно почленно интегрировать и дифференцировать любое число раз.
Так как степенной ряд для своей суммы есть ряд Тейлора, то полученное в результате указанных действий разложение будет искомым.
 2020-06-08
2020-06-08 104
104







