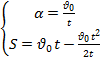Задача 1. Велосипедист, едущий со скоростью 18 км/ч, начинает спускаться с горы. Определить скорость велосипедиста через 6 с, если ускорение равно 0,8 м/с2.
| Дано: | СИ: | Решение: |
 0 = 18 км/ч 0 = 18 км/ч
| = 5 м/с |
|
| t = 6 с | ||
| α = 0,8 м/с2 | ||
| Найти: | Движение велосипедиста равноускоренное, т.е. α >0. | |
 -? -?
| Ось 0x направим по направлению движения велосипедиста. | |
Скорость можно определить по формуле  = = 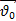 + + 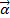 t. t.
| ||
С учётом знаков проекций на ось 0x формула скорости примет вид: 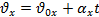 . .
| ||
| Вычислим значение скорости: | ||
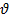 =5+0,8·6=9,8 м/с =5+0,8·6=9,8 м/с
| ||
| Ответ: | 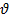 =9,8 м/с =9,8 м/с
|
Задача 2. Поезд через 20 с после начала движения приобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с?
| Дано: | Решение: |
| t1=20 с | Движение поезда носит равноускоренный характер, скорость |
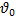 =0 =0
| Увеличивается, ускорение постоянно и положительно. |
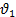 =0,6 м/с =0,6 м/с
| Найдём ускорение движения: 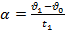 , т. к. , т. к. 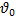 =0, то =0, то 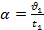 . .
|
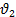 =3 м/с =3 м/с
| Пользуясь формулой ускорения, найдём второй промежуток времени: |
| Найти: | 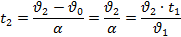
|
| t2 -? | t2= 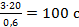
|
| Ответ: | t2=100 с |
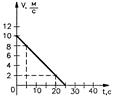
Задача 3. Скорость автомобиля за 10 с уменьшилась с 10 до 6 м/с. Написать формулу зависимости 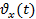 скорости от времени, построить график этой зависимости и по графику определить скорость через 20 с.
скорости от времени, построить график этой зависимости и по графику определить скорость через 20 с.
| Дано: | Решение: | ||||||
| t1=10 с | Скорость автомобиля уменьшается, следовательно, движение равнозамедленное, т.е. αx<0. Направление скорости движения | ||||||
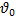 =10 м/с =10 м/с
| противоположно направлению ускорения. Уравнение проекции скорости | ||||||
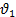 = 6 м/с = 6 м/с
| примет вид: 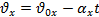 . .
| ||||||
| t2=20 с | Ускорение автомобиля найдём по формуле: 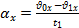 . .
| ||||||
| Найти: | 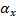 = = 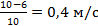 2 2
| ||||||
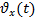 -? -?
| Уравнение скорости движения: 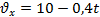 . .
| ||||||
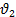 -? -?
| Построим график зависимости. Достаточно определить две точки, т.к. Графиком скорости является прямая линия. Можно составить таблицу:
| ||||||
|
| |||||||
| Через 20 с скорость автомобиля будет равна 2 м/с. | |||||||
| Ответ: | 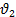 = 2 м/с, = 2 м/с, 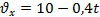 . .
|
Задача 4. Поезд движется со скоростью 20 м/с. При торможении до полной остановки он прошёл расстояние в 200 м. Определите время, в течение которого происходило торможение.
| Дано: | Решение: |
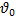 =20 м/с =20 м/с
| Движение поезда равнозамедленное, следовательно, в уравнениях для |
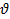 =0 =0
| проекции скорости и проекции перемещения перед проекцией ускорения |
| S=200 м | берётся знак "-". |
| Найти: | Запишем систему из двух уравнений и решим её относительно промежутка |
| t-? | времени t, учитывая, что 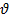 =0: =0:
|
|
| |
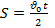 → → 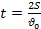
| |
| Вычислим время торможения: | |
t 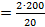 =20 с =20 с
| |
| Ответ: | Время торможения поезда 20 секунд. |
Задача 5. Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 2 м/с2 при скорости 72 км/ч?
| Дано: | СИ: | Решение: |
| αцс=2 м/с2 | Из формулы центростремительного ускорения определим | |
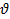 = 72 км/ч = 72 км/ч
| = 20 м/с | радиус кривизны закругления дороги: |
| Найти: | αцс= 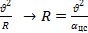
| |
| R-? | R= 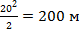
| |
| Ответ: | R=200 м |
Задание 2. Решите количественные задачи.
Задача 1. Прямолинейное движение двух тел задано уравнениями 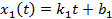 и
и 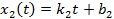 , где
, где 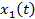 и
и 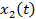 - координаты в момент времени t первого и второго тел соответственно. Охарактеризуйте движение тел. Определите время и координату их встречи. Численные значения величин приведены в Международной системе единиц (СИ).
- координаты в момент времени t первого и второго тел соответственно. Охарактеризуйте движение тел. Определите время и координату их встречи. Численные значения величин приведены в Международной системе единиц (СИ).
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
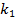
| 3 | 1 | 4 | 6 | 2,5 | 0,5 | 2 | 2 | 6 | 20 |
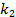
| 1 | 3 | 3 | 7 | 3 | 11 | 10 | 2 | 5 | 40 |
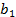
| 2 | 0,5 | 3 | 4 | 1,5 | 0,2 | 0,5 | 1 | 3 | 5 |
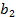
| 4 | 5 | 8 | 15 | 9 | 14 | 13 | 4 | 20 | 100 |
Задача 2. Материальная точка с начальной скоростью 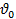 движется с ускорением α и через время t имеет скорость
движется с ускорением α и через время t имеет скорость 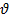 . Определите значение величины, обозначенной «?». Движение прямолинейное, вдоль одной координатной оси.
. Определите значение величины, обозначенной «?». Движение прямолинейное, вдоль одной координатной оси.
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
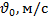
| 7,5 | 0,4 | ? | 16 | 2 | 0,8 | ? | 7 | 8 | 1,2 |
| α, м/с2 | 10 | 2 | 10 | ? | 5 | 4 | 0,5 | ? | 8 | 6,5 |
| t, с | ? | 1,5 | 2 | 0,5 | ? | 3 | 8 | 3 | ? | 4 |
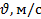
| 9,5 | ? | 80 | 18 | 3,5 | ? | 12 | 10 | 16 | ? |
Задача 3. Автомобиль, имевший начальную скорость 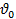 , разгоняется с ускорением α до скорости
, разгоняется с ускорением α до скорости 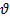 на пути длиной l. Определите значение величины, обозначенной «?». Сколько времени длится разгон?
на пути длиной l. Определите значение величины, обозначенной «?». Сколько времени длится разгон?
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| l, м | 60 | 50 | 40 | ? | 50 | 80 | 40 | ? | 100 | 100 |
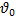 , м/с , м/с
| 10 | 5 | ? | 5 | 8 | 10 | ? | 10 | 15 | 15 |
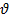 , км/ч , км/ч
| 72 | ? | 144 | 72 | 54 | ? | 72 | 144 | 108 | ? |
| α, м/с2 | ? | 4 | 2 | 3 | ? | 3 | 3 | 4,5 | ? | 2,5 |
Задача 4. По имеющимся в таблице данным укажите значения ускорения и начальной скорости, а также постройте графики зависимости перемещения, скорости и координаты от времени за первые 20 секунд. Определите значение величины, обозначенной «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
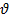 (t) = (t) =
| 5– 2t | ? | -3+ 2t | ? | 1 – 2t | ? | 5 – 3t | ? | 4 + 3t | ? |
| S(t) = | ? | 4t+0,5t2 | ? | 2t+1,5t2 | ? | 4t+1,5t2 | ? | -2t+t2 | ? | t+0,5t2 |
| x0, м | 2 | 0 | 1 | 2 | 5 | 4 | 2 | 3 | 1 | 2 |
Задача 5. Материальная точка движется со скоростью 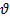 по окружности радиусом R, имея при этом центростремительное ускорение aц. За время t материальная точка проходит расстояние S, при этом совершая поворот на угол φ. Угловая скорость ω. Определите значение величины, обозначенной «?».
по окружности радиусом R, имея при этом центростремительное ускорение aц. За время t материальная точка проходит расстояние S, при этом совершая поворот на угол φ. Угловая скорость ω. Определите значение величины, обозначенной «?».
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
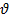 , м/с , м/с
| ? | 0,1 | ? | 0,5 | ? | 0,8 | 0,21 | 0,15 | ? | ? |
| R, м | 0,1 | ? | 0,4 | ? | ? | ? | 0,35 | 0,3 | ? | 0,45 |
| ац, м/с2 | ? | 7·10-4 | 0,225 | ? | ? | ? | ? | ? | 0,01 | ? |
| ω, об/с | 2 | ? | ? | 10 | ? | ? | ? | ? | ? | 0,78 |
| S, м | 0,314 | ? | ? | ? | 0,95 | ? | ? | 0,31 | 0,2 | ? |
| φ | ? | ? | π/6 | ? | 3 π /2 | 2 π | ? | ? | π /4 | ? |
| t, с | ? | 24 | ? | 0,08 | 2,35 | 1,25 | 7 | ? | ? | 0,69 |
Лабораторная работа №3
 2020-06-08
2020-06-08 678
678


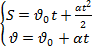 →
→ 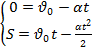 →
→