Как и на плоскости, отложим на каждой оси от начала координат в положительном направлении по вектору, длины которых будут равны 1. Эти векторы называют единичными, или ортами. Обозначают их соответственно 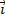 ,
, 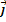 ,
, 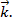 (См. Рис. 13.)
(См. Рис. 13.)
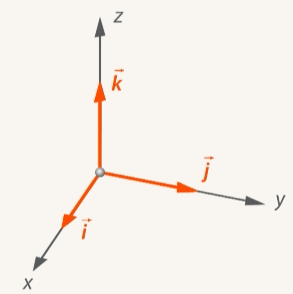
Рис. 13. Орты 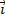 ,
, 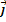 ,
, 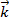
Эти векторы не компланарны, то есть не лежат в одной плоскости, а значит, каждый вектор пространства можно единственным образом разложить по векторам 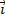 ,
, 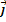 ,
, 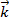 :
: 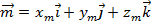 . Такие коэффициенты
. Такие коэффициенты 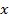 ;
; 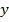 ;
; 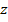 называют координатами вектора и пишут:
называют координатами вектора и пишут: 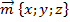 – в фигурных скобках. (См. Рис. 14.)
– в фигурных скобках. (См. Рис. 14.)
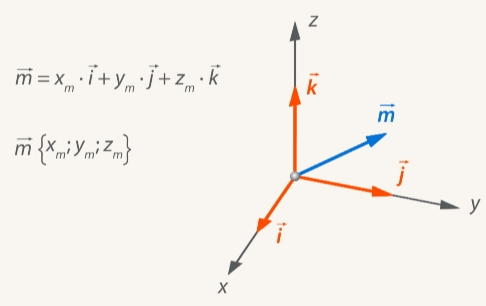
Рис. 14. Координаты вектора через орты
Так, например, вектор 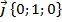 .
.
Заключение
На этом уроке мы познакомились с понятием «система координат в пространстве» и выяснили, как задаются координаты точки и координаты вектора.
Список литературы
1. Атанасян Л.С. и др. Геометрия. Учебник для 10–11 классов. – 18-е изд. – М.: Просвещение, 2009. – 255 с.
2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002
3. В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс, 2013
Дополнительные рекомендованные ссылки на ресурсы Интернет
1. Yaklass.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Alwebra.com.ua (Источник).
Домашнее задание
1. На каких расстояниях от координатных плоскостей находится точка 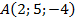
2. Определите, лежит ли данная точка на координатной оси. Если да, то укажите эту ось. 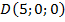 ,
, 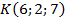 ,
, 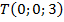 ,
, 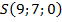 ,
, 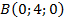
3. Определите, принадлежит ли данная точка координатной плоскости. Если да, то назовите ее. 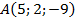 ,
, 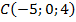 ,
, 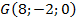 ,
, 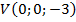 ,
, 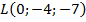 .
.
 2020-06-08
2020-06-08 124
124







