Координаты точки в пространстве

Оси обозначаются (ось абсцисс), (ось ординат) и (ось аппликат). (См. Рис. 8.)

Рис. 8. Названия координатных осей

Соответствующие плоскости – , , – координатные плоскости. (См. Рис. 9.) Как и на плоскости, у каждой оси в пространстве есть положительное направление и отрицательное.

Рис. 9. Координатные плоскости

Координаты точки в пространстве определяются аналогично плоскостным. Рассмотрим произвольную точку M и проведем через нее плоскости, параллельные координатным. Эти плоскости пересекут наши оси в точкахA (точка пересечения параллельной плоскости с осью OX), B (точка пересечения параллельной плоскости с осью OY) и C (точка пересечения параллельной плоскости с осью OZ). (См. Рис. 10.)

Рис. 10. Точки пересечения параллельных плоскостей с осями координат

Тогда абсцисса точки M – это OA(в случае если A лежит на положительной полуоси) и -OA, если A – на отрицательной. (См. Рис. 11.)

Рис. 11. Абсцисса точки M в зависимости от расположения точки A

Аналогично определяются ордината и аппликата. Записывают координаты в круглых скобках через точку с запятой: , где , , (либо , , – в зависимости от расположения на осях координат). Не пишите координаты точки через запятую, чтобы не спутать с десятичными дробями.

У точки могут быть и нулевые координаты, если она лежит в координатной плоскости. Например, если взять точку в плоскости , то ее координаты имеют вид . А точка на оси имеет координаты . Начало же координат – точка 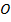– имеет координаты . (См. Рис. 12.)

Рис. 12. Точки с нулевыми координатами