ПРОСТЕЙШИЕ ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2.1. Поступательное движение твердого тела
Твердое тело состоит из бесконечного количества материальных точек, заполняющих некоторый объем без пустот. Если твердое тело движется, то вместе с ним движутся и все принадлежащие ему материальные точки. Уравнения движения твердого тела должны позволять в любой момент времени определить положение и кинематические характеристики любой его точки.
Простейшими видами движения твердого тела являются поступательное и вращательное движения.
Поступательным движением называется движение, при котором любой отрезок принадлежащий телу перемещается, оставаясь параллельным своему первоначальному направлению.
ТЕОРЕМА
Все точки твердого тела, движущегося поступательно, описывают тождественные, то есть совпадающие при наложении, траектории и в каждый момент времени имеют одинаковые скорости и одинаковые ускорения.
Доказательство
Пусть тело движется поступательно.
Выберем две точки А и В, проведя соответствующие радиус-векторы  и
и  . Покажем также вектор
. Покажем также вектор  , проведенный из точки А в точку В.
, проведенный из точки А в точку В.
 Рис. 2.1
Рис. 2.1
При поступательном движении вектор  не изменяет направления и не меняет длины (тело абсолютно твердое), то есть
не изменяет направления и не меняет длины (тело абсолютно твердое), то есть 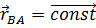 .
.
В этом случае траектория точки В получается сдвигом траектории точки А на вектор  . Две траектории будут тождественны.
. Две траектории будут тождественны.
Из рисунка видно, что  .
.
Продифференцируем равенство:  .
.
Так как 

 , то
, то 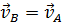 .
.
То есть в любой момент времени скорости всех точек равны по величине и направлению.
Дифференцируя равенство еще раз, получим, что  . Ускорения всех точек тела также векторно равны.
. Ускорения всех точек тела также векторно равны.
Теорема доказана.
ВЫВОД:
Поступательное движение твердого тела полностью определяется движением какой-либо его точки, например центра тяжести. В этом случае имеют смысл выражения «скорость тела» или «ускорение тела». При других формах движения каждая точка тела имеет свою скорость и свое ускорение.
2.2. Вращательное движение твердого тела
Движение тела, при котором все точки тела, лежащие на некоторой прямой, остаются неподвижными, называется вращательным движением. При этом сама прямая называется осью вращения.
Точки, не лежащие на оси, при движении описывают окружности в плоскостях, которые перпендикулярны к оси вращения.
Проведем через ось вращения полуплоскость, которая в начальный момент времени занимает положение П. В процессе вращения эта плоскость (рис. 2.2) будет поворачиваться на угол  , который меняется в зависимости от времени:
, который меняется в зависимости от времени:
 (2.1)
(2.1)
Уравнение (2.1) называется уравнением вращательного движения твердого тела.
Знак угла  определяется по правилу правого винта.
определяется по правилу правого винта.
Угол измеряется в радианах, то есть 
Основные кинематические характеристики такого движения - угловая скорость иугловое ускорение.
Угловой скоростью называется лежащий на оси вращения вектор  , проекция которого на эту ось равна производной по времени от угла поворота:
, проекция которого на эту ось равна производной по времени от угла поворота:
 . (2.2)
. (2.2)
Эта проекция называется алгебраическим значением угловой скорости.
Модуль угловой скорости равен  , а его размерность
, а его размерность  .
.

Рис. 2.2 Рис. 2.3
При  угол поворота
угол поворота  увеличивается, а при
увеличивается, а при  уменьшается.
уменьшается.
В технике угловую скорость часто измеряют в оборотах в минуту, обозначая ее буквой «n». Связь между n и ω дается формулой:
 .
.
Угловым ускорением называется величина  , равная производной по времени от угловой скорости:
, равная производной по времени от угловой скорости:

При этом проекция вектора углового ускорения на ось z будет равна
 . (2.3)
. (2.3)
Она называется алгебраическим значением углового ускорения.
Модуль углового ускорения равен
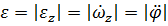 .
.
Его размерность  .
.
Знаки углового ускорения и угловой скорости позволяют установить является вращение замедленным или ускоренным (рис. 2.3).
При  вращение является ускоренным (направления векторов совпадают), а при
вращение является ускоренным (направления векторов совпадают), а при  – замедленным (направления векторов противоположны).
– замедленным (направления векторов противоположны).
Угловая скорость и угловое ускорение характеризуют вращение тела, как целого. Скорости и ускорения отдельных точек тела при этом будут отличаться.
2.3. Равномерное и равнопеременное вращение
Равномерным называется такое вращение тела, при котором угловая скорость все время остается постоянной:  . Тогда
. Тогда  .
.
При равномерном вращении  . Интегрируя это равенство, получим уравнение равномерного вращения:
. Интегрируя это равенство, получим уравнение равномерного вращения:
 .
.
Это уравнение определяет величину угла поворота в любой момент времени.
Равнопеременным называется вращение тела, при котором величина углового ускорения все время остается постоянной:  Оно бывает равноускоренным или равнозамедленным.
Оно бывает равноускоренным или равнозамедленным.
Дважды интегрируя равенство  получим выражения для угловой скорости и угла поворота, то есть уравнения равнопеременного вращения:
получим выражения для угловой скорости и угла поворота, то есть уравнения равнопеременного вращения:
 ;
;  ,
,
где  и
и  − начальные значения угла поворота и угловой скорости.
− начальные значения угла поворота и угловой скорости.
2.4 Скорость точки вращающегося тела
Рассмотрим твердое тело, совершающее вращение вокруг оси z (рис. 2.4).
Точки, лежащие на оси вращения, при этом будут находиться в неподвижности. Любая точка М, не лежащая на оси вращения, будет двигаться по окружности, которая лежит в плоскости, перпендикулярной к оси вращения z.

Рис. 2.4
Рассмотрим, как найти скорость и ускорение точки М, которая удалена от оси вращения на расстояние R, если для вращающегося тела известна угловая скорость  и угловое ускорение
и угловое ускорение  (рис. 2.4).
(рис. 2.4).
Найдем скорость точки М.
Глядя навстречу оси вращения покажем траекторию точки М (рис. 2.5).

Рис. 2.5
За начало отсчета дуговой координаты s примем точку О, которая лежит в неподвижной полуплоскости П. Подвижную полуплоскость П1 проведем через точку М.
Положительное направление отсчета дуговой координаты s пусть соответствует правилу правого винта.
Из геометрии известно соотношение между углом и длиной дуги:  .
.
Дифференцируя его по времени, найдем скорость точки:
 .
.
Для модулей соответствующих скоростей получим:
 (2.4)
(2.4)
Ясно, что модули скоростей точек пропорциональны их расстояниям до оси вращения, а коэффициентом пропорциональности является модуль угловой скорости.
2.5. Ускорение точки вращающегося тела
Найдем ускорение точки М.
Из кинематики точки известно, что полное ускорение является векторной суммой касательного и нормального ускорений (рис. 2.6):
 ,
,
где  - касательное ускорение, которое при рассмотрении твердого тела называют вращательным ускорением,
- касательное ускорение, которое при рассмотрении твердого тела называют вращательным ускорением,
 - нормальное ускорение, которое при рассмотрении твердого тела называют центростремительным ускорением.
- нормальное ускорение, которое при рассмотрении твердого тела называют центростремительным ускорением.
В ряде книг вместо  применяются обозначения
применяются обозначения  и
и  .
.
Найдем алгебраическое значение вращательного ускорения:
 R.
R.
При этом модуль вращательного ускорения:
 (2.5)
(2.5)
Центростремительное ускорение определяется по формуле:
 ,
,
Откуда  R. (2.6)
R. (2.6)

Рис. 2.6
Понятно, что при ускоренном вращении скорость точки и ее вращательное ускорение будут направлены в одну сторону, а при замедленном вращении – в разные, как это показано на рис. 2.6.
2.6. Скорость и ускорение точки вращающегося тела
в векторной форме
Формулы для определения скорости и ускорения точки вращающегося тела могут быть представлены в векторной форме.
Выберем на оси вращения произвольную точку О (рис. 2.7). Положение произвольной точки М, которая при вращении тела описывает окружность радиусом R, укажем с помощью радиус-вектора  , проведенного из точки О.
, проведенного из точки О.
Рассмотрим вектор  .
.
По модулю этот вектор равен скорости, так как
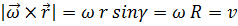 .
.
Направление этого вектора тоже совпадает с направлением скорости.
Поэтому справедливо равенство
 . (2.9)
. (2.9)
Формула (2.9) известна как формула Эйлера, которая позволяет определить скорость произвольной точки вращающегося тела.
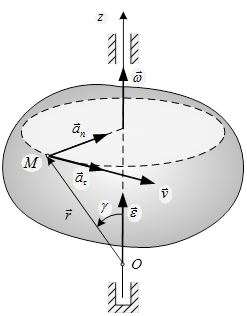
Рис. 2.7
Дифференцируя ее по времени найдем ускорение точки М:
 .
.
Первое слагаемое определяет касательное (вращательное) ускорение:
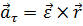 , (2.10)
, (2.10)
а второе представляет собой нормальное (центростремительное) ускорение:
 (2.11)
(2.11)
Полное ускорение равняется их векторной сумме.
2.7. Преобразование форм движения
В движущихся элементах машин часто происходят преобразования движений:
· преобразование одного вращательного движения в другое, а также
· преобразование вращательного движения в поступательное
(и наоборот).
Преобразования эти происходят с помощью
· зубчатых или фрикционных передач (рис. 2.8,а, рис. 2.8,в)
· ременных или цепных передач (рис. 2.8,б)
Связи между скоростями двух различных движений называются кинематическими связями.
 Рис. 2.8
Рис. 2.8
Они устанавливаются из условия отсутствия проскальзывания между взаимодействующими телами, то есть из условия равенства скоростей двух тел в точке их соприкосновения.
Так для рис. 2.8,а справедливым является соотношение
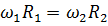 или
или  , (2.12)
, (2.12)
которое получено из условия, что в точке соприкосновения  (скорость точки первого тела равна скорости точки второго тела).
(скорость точки первого тела равна скорости точки второго тела).
В соответствии с этим соотношением, угловые скорости обратно пропорциональны соответствующим радиусам.
В случае зубчатой передачи, в которой зацепляются зубчатые колеса с числом зубьев  , такое же по смыслу равенство можно записать в виде:
, такое же по смыслу равенство можно записать в виде:
 .
.
Для передачи, показанной на рис. 2.8,в, имеем соотношение
 .
.
Тема: ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
3.1. Задание плоского движения
Плоскопараллельным или плоским движением называется движение твердого тела, при котором его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Установим способ задания плоского движения.
Рассмотрим тело, совершающее плоское движение относительно неподвижной плоскости Оху (рис.3.1). Выделим в теле два сечения: сечение S в плоскости Оху и сечение S’ в плоскости О’х’у’. Рассмотрим отрезок, соединяющий точки М и М', которые принадлежат соответственно сечениям S и S'. Пусть отрезок ММ' будет перпендикулярен к выбранным сечениям.
В процессе движения точка М не будет выходить из плоскости Оху, а точка М' – из плоскости О’х’у’. Сам отрезок в любой момент времени будет параллельным оси z, и его движение, следовательно, является поступательным. Отсюда следует, что все точки отрезка ММ' движутся одинаково.
Тогда для описания движения отрезка ММ' достаточно описать движение только одной точки, например, точки М. Следовательно, для описания движения всего тела достаточно описать движение только одного сечения, например, сечения S.
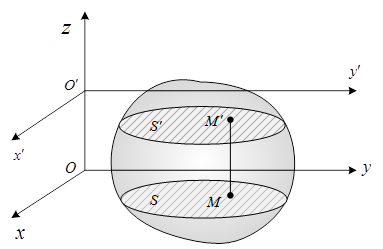
Рис. 3.1
 2020-06-08
2020-06-08 175
175







