Вывод: описание плоскопараллельного движения тела сводится к описанию движения одного сечения тела (плоской фигуры) относительно неподвижной плоскости

Рассмотрим движение плоской фигуры (рис. 3.2). Для этого выберем неподвижную систему координат Оху. Выберем на плоской фигуре точку С, которую будем называть полюсом и проведем через нее систему координат, которая будет двигаться вместе с телом.

Положение точки С в любой момент времени определяется координатами полюса. Само тело при этом может поворачиваться вокруг полюса. Величину этого поворота определяет угол  (угол между осями х и х').

Рис.3.2

Координаты полюса и угол поворота при движении меняются, то есть зависят от времени. Соответствующие формулы называются уравнениями плоскопараллельного движения:

                                                              (3.1)

Из этих уравнений можно найти основные кинематические характеристики тела при плоском движении:

· скорость и ускорение полюса,

· угловую скорость и угловое ускорение тела.

Важно заметить, что:

· плоское движение можно представить как совокупность двух движений: поступательного и вращательного,

· угол поворота () и кинематические характристики вращательной части движения ( и ) не зависят от выбора полюса,

· координаты полюса (, ) и кинематические характеристики поступательной части движения ( и ) зависят от выбора полюса.

Уравнения (3.1) позволяют найти скорость и ускорение полюса ( и ). Ниже рассмотрим, как найти скорости и ускорения других точек тела.

3.2. Теорема о сложении скоростей при плоском движении

ТЕОРЕМА

Скорость точки плоской фигуры равна векторной сумме скорости полюса и скорости, которую эта точка имеет в относительном вращении этой фигуры вокруг полюса:

            .                                               (3.2)

Доказательство

Рассмотрим плоскую фигуру. Выберем на ней две точки С и М. Точку С будем считать полюсом (рис. 3.3). Покажем радиус-векторы и , а также вектор , проведенный из точки С к точке М.

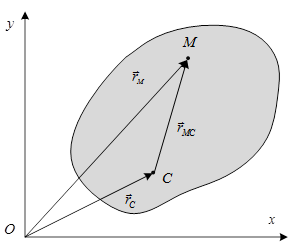
Рис. 3.3

Для любого момента времени справедливым будет равенство

            .

Дифференцируя равенство, получим:

            ,

где   - скорость точки М,

   - скорость точки С,

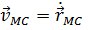- скорость точки М в движении тела, происходящем относительно полюса С.   Это движения является вращением, поскольку модуль вектора .

Теорема доказана.

Направление и модуль вектора  определяется по правилам, принятым для вращательного движения:

·  скорость перпендикулярна отрезку МС и направлена в сторону вращения,

· модуль скорости вычисляется по формуле Эйлера:

                                                        (3.3)

Графически направление и модуль скорости можно получить, построив параллелограмм на векторах и , как это показано на рис. 3.4,а.

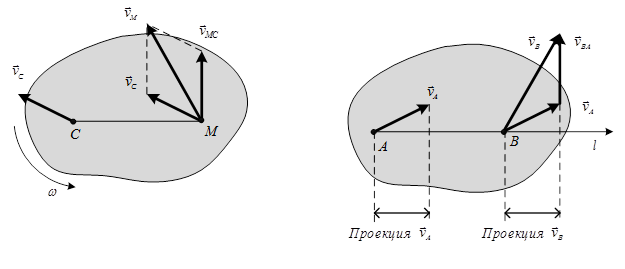      Рис. 3.4                                                                            Рис. 3.5

 

СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ: