Часть 2
Задача N 21
На вход интегратора в момент  подается стационарный случайный процесс
подается стационарный случайный процесс 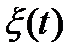 с
с  и функцией корреляции
и функцией корреляции  . Процесс на выходе:
. Процесс на выходе: 
1) Определить общие выражения для функции корреляции 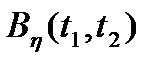 и дисперсии
и дисперсии  процесса
процесса 
2) Вычислить дисперсию  для случая
для случая 
3) Вычислить дисперсию для случая, когда 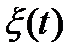 - белый шум с
- белый шум с  и спектральной плотностью
и спектральной плотностью  (т.е.
(т.е.  - винеровский случайный процесс)
- винеровский случайный процесс)
4) Построить графики функции  для случаев (2) и (3).
для случаев (2) и (3).
Задача N 22
Осуществляется линейное преобразование случайного процесса 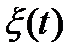 , при этом
, при этом  , где
, где  . Процесс
. Процесс 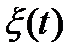 имеет плотность вероятности
имеет плотность вероятности  . Найти общее выражение для плотности вероятности
. Найти общее выражение для плотности вероятности  и конкретизировать его для случая, когда
и конкретизировать его для случая, когда 
Задача N 23
Используя интегральное уравнение Винера-Хопфа получить соотношение для функции передачи оптимального сглаживающего фильтра с бесконечной задержкой.
Задача N 24
Показать, что согласованный фильтр обеспечивает максимальное значение отношения сигнал/шум на выходе при наличии аддитивного белого шума на входе.
Задача N 25
Стационарный случайный процесс 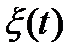 имеет плотность вероятности
имеет плотность вероятности
 (распределение Релея).
(распределение Релея).
Определить плотность вероятности 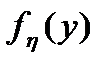 процесса
процесса 
Задача N 26
Стационарный случайный процесс 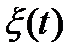 имеет плотность вероятности:
имеет плотность вероятности:

Найти плотность вероятности 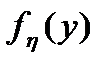 процесса
процесса  . Получить также
. Получить также 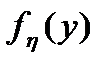 для частного случая
для частного случая  .
.
Задача N 27
Случайный процесс 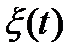 имеет плотность вероятности
имеет плотность вероятности 
Найти плотности вероятности процессов:
1) на выходе диода с характеристикой 
2) на выходе идеального линейного детектора с характеристикой
 , где
, где 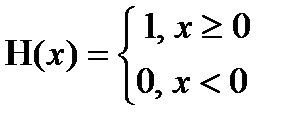 - функция Хевисайда
- функция Хевисайда
Задача N 28
Определить двумерную плотность вероятности процесса  на выходе безинерционного нелинейного устройства, если
на выходе безинерционного нелинейного устройства, если  ,
, 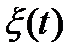 - нормальный случайный процесс с
- нормальный случайный процесс с  и ковариационной функцией
и ковариационной функцией 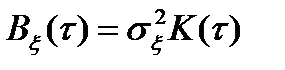 .
.
Задача N 29
Нормальный случайный процесс 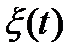 , имеющий спектральную плотность
, имеющий спектральную плотность  пропускается через нелинейное устройство. Процесс на выходе
пропускается через нелинейное устройство. Процесс на выходе  .
.
Определить спектральную плотность процесса  , если
, если 
Построить график  .
.
Задача N 30
Нормальный стационарный случайный процесс 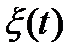 имеет
имеет  и функцию корреляции
и функцию корреляции 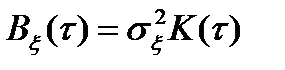 , где
, где  - коэффициент корреляции. Найти плотность вероятности
- коэффициент корреляции. Найти плотность вероятности 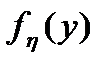 частного от деления двух зависимых значений случайного процесса
частного от деления двух зависимых значений случайного процесса  .
.
Задача N 31
Пусть на плоский экран с двумя параллельными щелями (двухщелевой интерферометр), расположенный в плоскости YZ, перпендикулярно падает узкополосная случайная волна (см. рис.)
 , где с - скорость волны,
, где с - скорость волны,
с ковариационной функцией (в фиксированной точке х)

| θ |
| d |
| ξ 1 |
| ξ 2 |
| R |
| x |
| y |
| ξ |
За экраном на большом расстоянии от щелей  измеряется средняя интенсивность суммарного сигнала от двух щелей в зависимости от угла θ (интерференционная картина)
измеряется средняя интенсивность суммарного сигнала от двух щелей в зависимости от угла θ (интерференционная картина)

где  .
.
1) Получить формулу для интерференционной картины 
2) Определить угловое расстояние между интерференционными полосами
3) Оценить угловой размер интерференционной картины
Задача N 32
Гауссовский белый шум 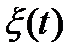 с нулевым средним значением и спектральной плотностью
с нулевым средним значением и спектральной плотностью  подается на интегратор. На выходе интегратора
подается на интегратор. На выходе интегратора 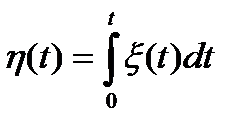
1) Найти плотность вероятности  процесса
процесса  .
.
2) Записать уравнение Фоккера-Планка для плотности вероятности  процесса
процесса  .
.
Задача N 33
Определить корреляцию  приращений
приращений 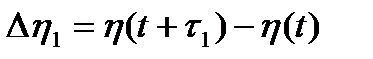 ,
,  на примыкающих неперекрывающихся интервалах времени
на примыкающих неперекрывающихся интервалах времени  и
и  для марковского случайного процесса, определяемого дифференциальным уравнением первого порядка
для марковского случайного процесса, определяемого дифференциальным уравнением первого порядка

( - постоянные,
- постоянные,  - гауссовский белый шум со спектральной плотностью
- гауссовский белый шум со спектральной плотностью 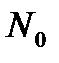 ), в установившемся режиме при малых (
), в установившемся режиме при малых ( ) и больших (
) и больших (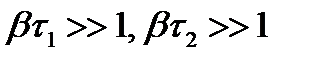 ) интервалах
) интервалах  и
и  .
.
Задача N 34
Нелинейная система описывается стохастическим уравнением  , где
, где 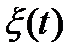 - белый шум с нулевым средним значением и спектральной плотностью
- белый шум с нулевым средним значением и спектральной плотностью  ,
,  .
.
1) Найти коэффициенты сноса и диффузии и записать уравнение Фоккера-Планка для плотности вероятности  процесса
процесса  .
.
2) Упростить уравнение Фоккера-Планка пренебрегая быстрыми осцилляциями.
3) Записать упрощенное стохастическое уравнение для системы.
Задача N 35
Получить выражение для стационарной плотности вероятности  марковского случайного процесса
марковского случайного процесса  , заданного стохастическим дифференциальным уравнением:
, заданного стохастическим дифференциальным уравнением:
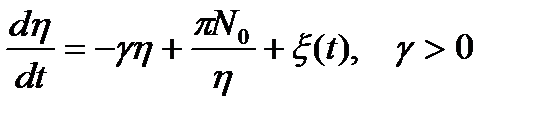
где  ,
, 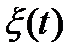 - белый шум с нулевым средним значением и спектральной плотностью
- белый шум с нулевым средним значением и спектральной плотностью  .
.
Задача N 36
Получить выражение для стационарной плотности вероятности  марковского случайного процесса
марковского случайного процесса  , заданного стохастическим дифференциальным уравнением:
, заданного стохастическим дифференциальным уравнением:
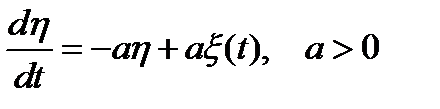
где 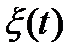 - белый шум с нулевым средним значением и спектральной плотностью
- белый шум с нулевым средним значением и спектральной плотностью  .
.
Задача N 37
Пусть  -мерный случайный процесс
-мерный случайный процесс 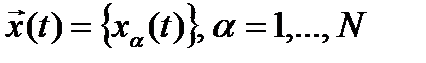 удовлетворяет системе стохастических уравнений
удовлетворяет системе стохастических уравнений
 ,
,
где  - независимые гауссовские случайные воздействия, имеющие свойства белого шума:
- независимые гауссовские случайные воздействия, имеющие свойства белого шума:  .
.
Записать уравнение Фоккера – Планка – Колмогорова для совместной плотности вероятностей  и показать, что стационарное решение этого уравнения имеет вид распределения Больцмана
и показать, что стационарное решение этого уравнения имеет вид распределения Больцмана  (константа
(константа  определяется из условия нормировки).
определяется из условия нормировки).
Задача N 38
Случайный процесс определяется стохастическим дифференциальным уравнением 2-го порядка
 ,
,
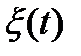 - гауссовский белый шум со спектральной плотностью
- гауссовский белый шум со спектральной плотностью  .
.
Записать эквивалентную систему 2-х стохастических дифференциальных уравнений 1-го порядка для  и
и  . Получить соответствующее уравнение Фоккера – Планка – Колмогорова для совместной плотности вероятностей
. Получить соответствующее уравнение Фоккера – Планка – Колмогорова для совместной плотности вероятностей 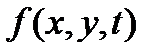 и показать, что стационарное решение этого уравнения имеет вид распределения Максвелла-Больцмана
и показать, что стационарное решение этого уравнения имеет вид распределения Максвелла-Больцмана  (константа
(константа  определяется из условия нормировки). Определить точки максимума
определяется из условия нормировки). Определить точки максимума  для потенциала
для потенциала 
Задача N 39
Получить соотношение для среднего времени достижения границ винеровским случайным процессом.
Задача N 40
Пуассоновский случайный процесс  определяет, сколько случайных событий произойдет на интервале
определяет, сколько случайных событий произойдет на интервале  , причем
, причем 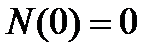 и вероятность состояния N в момент времени t дается распределением Пуассона
и вероятность состояния N в момент времени t дается распределением Пуассона 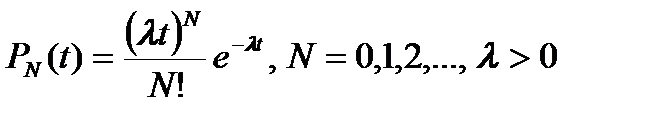 .
.
1) Получить дифференциальные уравнения, описывающие эволюцию во времени вероятностей состояний 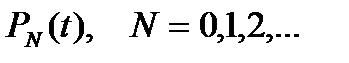
2) Найти среднее время пребывания процесса в неизменном состоянии.
 2020-06-08
2020-06-08 78
78







