1. В.Н. Тутубалин Теория вероятностей, М:., Издательский центр «Академия», 2008
2. С.А.Ахманов, Ю.Е.Дьяков, А.С.Чиркин. Статистическая радиофизика и оптика. Случайные колебания и волны. М: «Физматлит», 2010
3. Ю.А. Розанов. Введение в теорию случайных процессов, М: «Наука», 1982.
4. С.М. Рытов. Введение в статистическую радиофизику. ч.1. Случайные процессы. М: «Наука», 1976.
5. Б.Р. Левин. Теоретические основы статистической радиотехники. М: «Радио и связь», 1989.
Пособия и методические указания.
- А.В. Булинский. Случайные процессы. Примеры, задачи, упражнения. М: МФТИ, 2010
- Б.М. Миллер, А.Р.Панков, Теория случайных процессов в примерах и задачах. М: «Физматлит», 2002
Программу составил
В.Н.Лагуткин, д.т.н., доцент
«_____»_________2012 г.
Задание на курсовую работу по «Теории случайных процессов»
Часть 1
Задача N 1
Пусть конечное множество элементарных событий  составляют равновероятные события вида
составляют равновероятные события вида  , где каждое
, где каждое  может принимать значения 0 или 1, а случайная величина
может принимать значения 0 или 1, а случайная величина  определяется формулой
определяется формулой  (т.е. в двоичной системе
(т.е. в двоичной системе  ). Определить множество значений
). Определить множество значений  такой случайной величины и ее распределение вероятностей.
такой случайной величины и ее распределение вероятностей.
Задача N 2
Используя теорему о дифференцировании интегралов, зависящих от параметров, получить соотношение, связывающее моментные и характеристические функции


Задача N 3
Нормальный случайный процесс 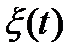 в момент
в момент  имеет плотность вероятности
имеет плотность вероятности

1) Найти характеристическую функцию  .
.
2) Вычислить математическое ожидание  и центральные моменты
и центральные моменты  , используя
, используя  .
.
3) Определить характеристическую функцию и плотность вероятности суммы независимых случайных величин  процесса:
процесса: 
Задача N 4
1) Показать, что для непрерывного случайного процесса с независимыми приращениями  ковариационная функция
ковариационная функция  связана с дисперсией
связана с дисперсией  соотношением
соотношением  ,
,
2) Получить выражения для многомерных распределений винеровского и пуассоновского случайных процессов.
Задача N 5
Двоичный счетчик пуассоновского потока частиц в каждом такте выдает значение  , если в течении длительности такта τ не пришло ни одной частицы, и значение
, если в течении длительности такта τ не пришло ни одной частицы, и значение  , если пришла одна или более частиц.
, если пришла одна или более частиц.
1) Как оценить среднюю частоту пуассоновского потока частиц λ имея запись случайной последовательности  нулей и единиц?
нулей и единиц?
2) Как зависит точность оценки средней частоты λ от длины записи N?
Задача N 6
Реализации случайного телеграфного процесса  представляют собой кусочно-постоянные знакопеременные функции, принимающие два значения (С и -С):
представляют собой кусочно-постоянные знакопеременные функции, принимающие два значения (С и -С):  , где
, где  - реализации пуассоновского случайного процесса, приращения которого
- реализации пуассоновского случайного процесса, приращения которого  на произвольных интервалах времени
на произвольных интервалах времени  являются случайными величинами, имеющими пуассоновское распределение с интенсивностью λ:
являются случайными величинами, имеющими пуассоновское распределение с интенсивностью λ:  .
.
Получить выражения для математического ожидания  и корреляционной функции
и корреляционной функции  телеграфного процесса.
телеграфного процесса.
Задача N 7
Установить условия стационарности (в широком смысле) действительного случайного процесса.
 ,
,
где  - случайные величины (
- случайные величины ( - не случайная).
- не случайная).
Записать выражение для ковариационной функции 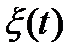 при этих условиях.
при этих условиях.
При каком дополнительном условии этот процесс является эргодическим относительно среднего значения?
Задача N 8
Найти спектральную плотность случайного процесса с ковариационной функцией:
1)  ;
;
2)  ;
;
3)  ;
;
Задача N 9
Пусть пуассоновский импульсный процесс задается соотношением
 ,
,
где  ,
,
 – моменты появления импульсов в рассматриваемом пуассоновском потоке импульсов,
– моменты появления импульсов в рассматриваемом пуассоновском потоке импульсов,
все случайные величины  ,
,  – статистически независимы между собой, имеют нулевое среднее значение и одинаковую дисперсию
– статистически независимы между собой, имеют нулевое среднее значение и одинаковую дисперсию  .
.
1) Определить среднее значение, дисперсию, ковариационную функцию и спектральную плотность такого процесса.
2) Построить график спектральной плотности  для случая
для случая  .
.
Задача N 10
1) Доказать, что не существует стационарного случайного процесса, корреляционная функция которого постоянна на интервале  и равна нулю вне этого интервала, т. е.
и равна нулю вне этого интервала, т. е.

2) Найти спектральную плотность случайного процесса с ковариационной функцией

Задача N 11
Показать, что случайный процесс  , где
, где  и
и  - постоянные фиксированные величины, а фаза
- постоянные фиксированные величины, а фаза  - случайная величина с плотностью вероятности
- случайная величина с плотностью вероятности  является стационарным в широком смысле.
является стационарным в широком смысле.
Задача N 12
Показать, что комплексный случайный процесс
 ,
,
где А – комплексная случайная величина со средним  и дисперсией
и дисперсией  , а ω – независимая от А действительная случайная величина с плотностью распределения
, а ω – независимая от А действительная случайная величина с плотностью распределения  , является стационарным в широком смысле. Определить спектральную плотность этого процесса.
, является стационарным в широком смысле. Определить спектральную плотность этого процесса.
Задача N 13
Определить ковариационную функцию и спектральную плотность теплового излучения  объема газа.
объема газа.
Считать, что излучение представляет собой комплексный пуассоновский импульсный процесс  с функцией импульсов
с функцией импульсов
 ,
,
где u – случайные скорости излучающих молекул газа, имеющие распределение Максвелла с температурой Т.
Задача N 14
Какому условию должна удовлетворять спектральная плотность стационарного случайного процесса, чтобы этот процесс обладал первой производной?
С помощью теоремы Винера-Хинчина определить при каких значениях коэффициента  функция
функция  может быть ковариационной функцией:
может быть ковариационной функцией:
1) стационарного случайного процесса?
2) дифференцируемого стационарного случайного процесса?
Задача N 15
Случайный процесс  , где
, где  - независимые стационарные случайные процессы с нулевыми средними и спектральными плотностями
- независимые стационарные случайные процессы с нулевыми средними и спектральными плотностями  соответственно. Найти спектральную плотность
соответственно. Найти спектральную плотность  процесса
процесса  .
.
Задача N 16
Определить математические ожидания, дисперсии и ковариационные функции комплексных случайных процессов  , где:
, где:
а)  - действительный стационарный нормальный случайный процесс с нулевым математическим ожиданием
- действительный стационарный нормальный случайный процесс с нулевым математическим ожиданием  и ковариационной функцией
и ковариационной функцией  ,
,
б)  - винеровский случайный процесс.
- винеровский случайный процесс.
Задача N 17
Нормальный стационарный случайный процесс 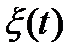 имеет
имеет  и корреляционную функцию
и корреляционную функцию  . Определить корреляционную функцию
. Определить корреляционную функцию  и плотность вероятности
и плотность вероятности  производной процесса
производной процесса  .
.
Использовать полученные результаты для приближенной оценки продольного углового размера лунной дорожки, наблюдаемой на взволнованной водной поверхности.
Задача N 18
Белый шум 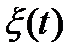 с
с  и спектральной плотностью
и спектральной плотностью  действует на RC фильтр.
действует на RC фильтр.
| C |

|
| R |

|
Найти:
1) частотную характеристику  и импульсную реакцию фильтра
и импульсную реакцию фильтра  ,
,
2) ковариационную функцию, дисперсию, спектральную плотность выходного процесса  в установившемся режиме,
в установившемся режиме,
3) дисперсию  в переходном режиме.
в переходном режиме.
Задача N 19
Дана линейная цепь - фильтр LR
| R |

|
| L |

|
 процесса
процесса 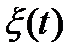 на входе фильтра LR при условии, что выходное напряжение
на входе фильтра LR при условии, что выходное напряжение  представляет собой стационарный случайный процесс с ковариационной функцией
представляет собой стационарный случайный процесс с ковариационной функцией 
Задача N 20
Дана параллельная цепочка RC
Найти:
1. Спектральную плотность по положительным частотам  напряжения теплового шума
напряжения теплового шума  на емкости C.
на емкости C.
2. Построить график зависимости  от величины R для трех частот: f=100Гц, 1.5 кГц, 15 кГц при C=100пф.
от величины R для трех частот: f=100Гц, 1.5 кГц, 15 кГц при C=100пф.
3. Вычислить дисперсию шума в полосе частот  .
.
4. Определить дисперсию шума во всей полосе частот  .
.
 2020-06-08
2020-06-08 224
224








