IV Предел последовательности

ОПР. Число А называется пределом последовательности а₁, а₂, а₃, …, если, начиная с некоторого момента все члены этой последовательности будут сколь угодно мало отличаться от А.

Обозначают предел последовательности латинскими буквами lim (лимит)

    А =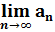   

Последовательности бывают:

1) сходящиеся (имеют предел)

2) расходящиеся (нет предела)

ОПР. Сходящаяся последовательность – это последовательность, у которой существует предел  

ОПР. Расходящаяся последовательность – это последовательность, не имеющая предела, а так же имеющая своим пределом

ОПР. (эпсилон) – окрестность точки а – это множество точек числовой прямой, если |х_n - а| ≤

 Геометрическое представление предела последовательности

Это означает, что при n > N все элементы последовательности {x_n} находятся в 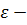 окрестности точки а.

Предел последовательности а, часто называют точкой сгущения.

Выводы:

1) Числовая последовательность может иметь только один предел.

2) Если последовательность имеет предел, то она ограничена.

3) Неограниченная последовательность не имеет конечного предела, но может иметь бесконечный предел.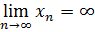

Свойства пределов.

V Бесконечно малая и бесконечно большие величины

ОПР. Переменная величина х_n имеющая своим пределом нуль, т.е.  называется бесконечно малой (б/м)

ОПР. Переменная величина х_n имеющая своим пределом бесконечность, т.е. 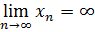 называется бесконечно большой (б/б)