Теоретическое введение

 

2

1

Рис. 6.1

C

R

L

~ U

Для осуществления вынужденных электромагнитных колебаний необходимо в реальный колебательный контур (рис. 6.1), содержащий катушку индуктивности L, конденсатор емкости C и активное сопротивление R, включить последовательно с элементами контура переменную ЭДС, или подать переменное  напряжение

U = U_m cosw t. (6.1)

Согласно закону Ома для неоднородного участка цепи 1–R–L–2 (рис. 6.1) получим

IR + (φ₁ – φ₂)=E_S +E(f),                       (6.2)

где φ₁ – φ_{2 =} q/C - разность потенциалов на обкладках конденсатора; E_S = - L(dI/dt) – ЭДС самоиндукции катушки индуктивности, E(f) = U₀cos ωt.

С учетом того, что I = 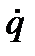 , и E_S = - L 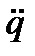, уравнение (6.2) принимает вид

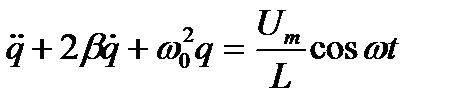                 (6.3)

где β = R/2L – коэффициент затухания, 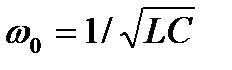 – частота собственных колебаний контура.

Уравнение (6.3) представляет собой стандартное дифференциальное уравнение вынужденных электромагнитных колебаний. При установившихся колебаниях дифференциальное уравнение (6.3) имеет решение

                 q = q_m cos(wt - y),                                (6.4)

где        

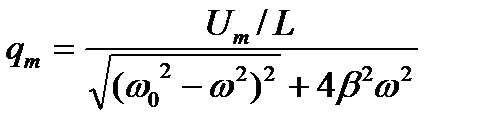,                 (6.5)

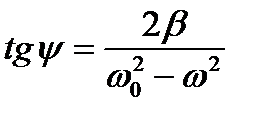                         (6.6)

Подстановка значений ω₀² и β дает

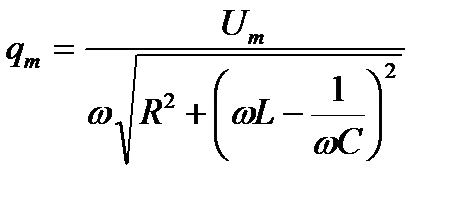,                (6.7)

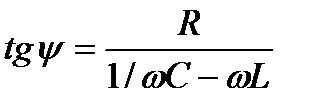                      (6.8)

Продифференцировав выражение (6.4) по t, найдем силу тока в контуре при установившихся колебаниях

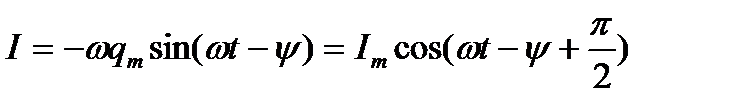         (6.9)

Запишем это выражение в виде

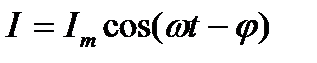,                          (6.10)

где φ=ψ-π/2 – есть сдвиг по фазе между током и приложенным напряжением. Амплитуду силы тока и начальную фазу найдем из формул (6.7) и (6.8)

(6.12)

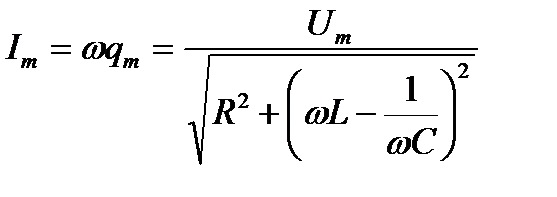             (6.11)

 

.             

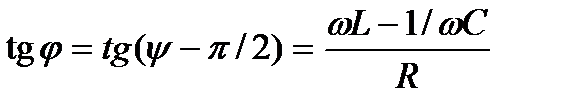Разделив выражение (6.4) на емкость, получим напряжение на конденсаторе

,           (13)

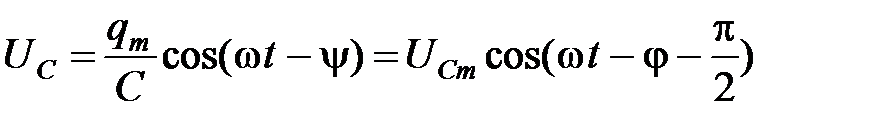     (6.13)

где

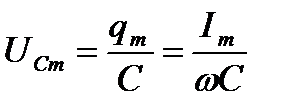.                     (6.14)

 

Умножив производную функции (6.10) на L, получим напряжение на индуктивности:

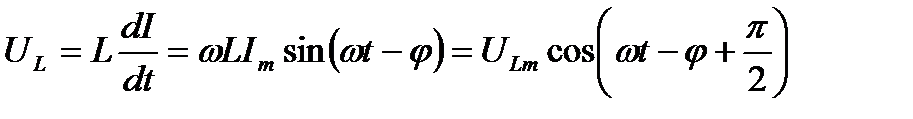,  (6.15)

где             

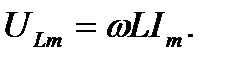                             (6.16)

Сопоставление формул (6.10), (6.13) и (6.15) показывает, что напряжение на емкости отстает по фазе от силы тока на π/2, а напряжение на индуктивности опережает ток на π/2.Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы (рис. 6.2).

Резонансная частота для заряда и напряжения на конденсаторе равна

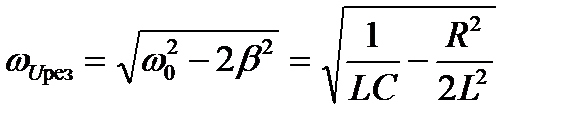.          (6.17)

 

Рис. 6.2

U

m

Um

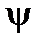
U

C

U

LI

w

C

I

m

w

L

U

I

ø

ö

è

æ

R

R

I

C

L

w

-

w

1

m

m

÷

ç

 

 

2

Резонансные кривые для U_с изображены на рис. 6.3. При ω→ 0 резонансные кривые сходятся в одной точке с ординатой U_Cm= U_m – напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения U_m.

Максимум при резонансе получается тем выше и острее, чем меньше β= R/2L.

Резонансные кривые для силы тока изображены на рис. 6.4.

Амплитуда силы тока имеет максимальное значение при 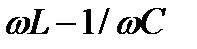=0. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура                              

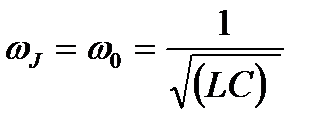                                (6.18)

 

 

 

 

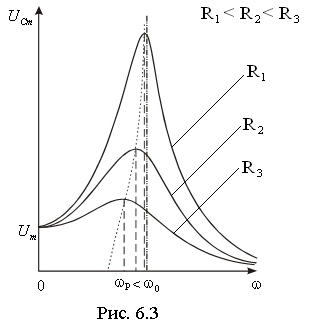
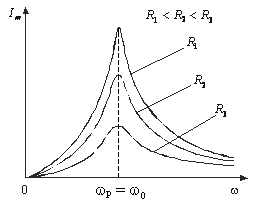
Рис. 6.4

 

При ω → 0, I_m = 0, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

4

Резонансные свойства контура характеризует добротность Q, которая показывает, во сколько раз напряжение на конденсаторе может превышать амплитудное значение приложенного напряжения, т.е.

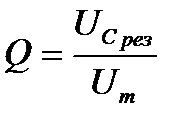                           (6.19)

При малых затуханиях ω_рез ≈ ω₀ и

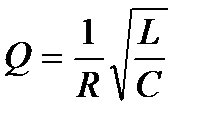                                             (6.20)

Таким образом, добротность обратно пропорциональна активному сопротивлению контура и определяет остроту резонансных кривых. На рис. 6.5 изображена одна из резонансных кривых для силы тока в контуре. Частоты ω₁ и ω₂ соответствуют току I = I_max/ .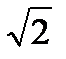

 

 

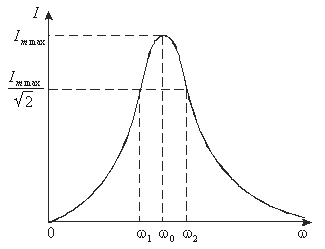
Рис. 6.5

 

Относительная ширина резонансной кривой равна величине обратной добротности контура, т. е.

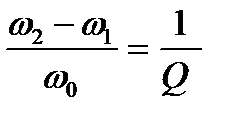                            (6.21)

5

Явление резонанса используют для выделения из сложного напряжения, равного сумме нескольких синусоидальных напряжений, нужной составляющей.

Пусть напряжение, приложенное к контуру, равно

U = U_{m 1}cos(w₁t + j₁) + U_{m 2}cos(w₂t + j₂) +…+ U_mi cos(w_it + j_i) +…+ U_mn cos(w _n t + j _n).

Настроив контур (посредством изменения R и C) на требуемую частоту w_i, можно получить на конденсаторе напряжение в Q раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет малым. Таким образом осуществляется, например, настройка радиоприёмника на нужную длину волны