Если некоторая функция f(x) определяется степенным рядом:  , то интеграл от этой функции можно записать в виде ряда:
, то интеграл от этой функции можно записать в виде ряда:
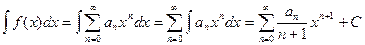
Дифференцирование степенных рядов.
Производная функции, которая определяется степенным рядом, находится по формуле:

Сложение, вычитание, умножение и деление степенных рядов.
Сложение и вычитание степенных рядов сводится к соответствующим операциям с их членами:
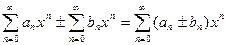
Произведение двух степенных рядов выражается формулой:
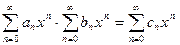
Коэффициенты сi находятся по формуле:
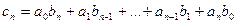
Деление двух степенных рядов выражается формулой:
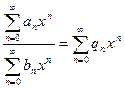
Для определения коэффициентов qn рассматриваем произведение  , полученное из записанного выше равенства и решаем систему уравнений:
, полученное из записанного выше равенства и решаем систему уравнений:
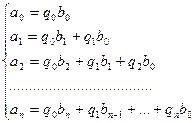
 2020-06-10
2020-06-10 111
111







