В технике широко применяются элементы конструкций, которые с точки зрения расчета на прочность и жесткость могут быть отнесены к тонким оболо-чкам. Принято считать оболочку тонкой, если отношение ее толщины к габа-ритному размеру меньше 1/20. Для тонких оболочек применима гипотеза пря-мых нормалей: отрезки нормали к срединной поверхности остаются прямыми и нерастяжимыми после деформирования. В этом случае имеет место линейное распределение деформаций, а следовательно и нормальных напряжений (при малых упругих деформациях) по толщине оболочки.
Поверхность оболочки получают вращением плоской кривой вокруг оси, лежащей в плоскости кривой. Если кривую заменить прямой линией, то при вращении ее параллельно оси получается круговая цилиндрическая оболочка, а при вращении под углом к оси - коническая.
В расчетных схемах оболочку представляют ее срединной поверхностью (равноудаленной от лицевых). Срединную поверхность обычно связывают с криволинейной ортогональной системой координаты Ө и φ. Углом θ (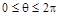 ) определяется положение параллели линии пересечения середин-ной поверхности с плоскостью, проходящей нормально к оси вращения.
) определяется положение параллели линии пересечения середин-ной поверхности с плоскостью, проходящей нормально к оси вращения.


Рис.11.6 Рис. 11.7
Через нормаль с серединой поверхности можно провести множество пло-скостей, которые будут нормальны к ней и в сечениях с ней образовывать ли-нии с разными радиусами кривизны. Два из этих радиусов имеют экстремаль-ное значения. Линии, которым они соответствуют, называются линиями главных кривизн. Одна из линий является медианой, её радиус кривизны обозначим r1. Радиус кривизны второй кривой – r2 (центр кривизны лежит на оси вращения). Центры радиусов r1 и r2 могут совпадать (сферическая оболоч-ка), лежать по одну или по разные стороны срединной поверхности, один из центров может уходить в бесконечность (цилиндрическая и коническая оболоч-ки).
При составлении основных уравнений усилия и перемещения относим к нормальным сечениям оболочки в плоскостях главных кривизн. Составим ура-внения для внутренних усилий. Рассмотрим бесконечно малый элемент оболо-чки (рис. 11.6), вырезанный двумя смежными меридиональными плоскостями (с углами θ и θ+dθ) и двумя смежными параллельными кругами, нормальными к оси вращения (с углами φ и φ+dφ). В качестве системы осей проекций и моментов избираем прямоугольную систему осей x, y, z. Ось y направлена по касательной к медиану, ось z – по нормали.
В силу осевой симметрии (нагрузка P=0) на элемент будут действовать только нормальные усилия. Nφ - погонное меридиональное усилие, направлен-ное по касательной к меридиану: Nθ - погонное кольцевое усилие, направлен-ное по касательной к окружности. Уравнение ΣХ=0 обращается в тождество. Спроектируем все силы на ось z:
2Nθr1dφ 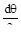 sinφ+[
sinφ+[ 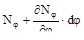 ]rodθdφ+Pzr1dφrodθ=0.
]rodθdφ+Pzr1dφrodθ=0.
Если пренебречь бесконечно малой величиной высшего порядка (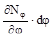 )ro dθ dφ и разделить уравнение на r1 ro dφ dθ, то принимая во внима-ние, что
)ro dθ dφ и разделить уравнение на r1 ro dφ dθ, то принимая во внима-ние, что 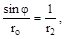 получим уравнение, принадлежащее П. Лапласу:
получим уравнение, принадлежащее П. Лапласу:
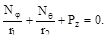
Вместо уравнения ΣY=0 для рассматриваемого элемента составим урав-нение равновесия верхней части оболочки (рис. 11.6). Спроектируем все силы на ось вращения:
Nφ 
uде: Rv- вертикальная проекция равнодействующей внешних сил, приложенных к отрезанной части оболочки. Итак,
Nφ= 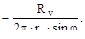
Подставив значения Nφ в уравнение Лапласа, найдём Nθ. Определение усилий в оболочке вращения по безмоментной теории представляет собой статически определимую задачу. Это стало возможным в результате того, что мы сразу постулировали закон изменения напряжений по толщине оболочки – считали их постоянными.
В случае сферического купола имеем r1= r2= r и rо= r 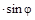 . Если нагрузка задана в виде интенсивности P на горизонтальную проекцию оболочки, то
. Если нагрузка задана в виде интенсивности P на горизонтальную проекцию оболочки, то
Rv= 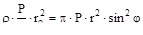 , и
, и
Nφ= 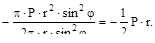
Таким образом, в меридиональном направлении купол равномерно сжат. Составляющие поверхностной нагрузки вдоль нормали z равна Pz=P 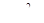 . Подставляем значения Nφ и Pz в уравнение Лапласа и находим из него:
. Подставляем значения Nφ и Pz в уравнение Лапласа и находим из него:
Nθ= 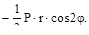
Кольцевые сжимающие усилия достигают максимума в вершине купола при φ = 0. При φ = 45º - Nθ=0; при φ > 45  - Nθ=0 становится растягивающим и достигает максимума при φ = 90
- Nθ=0 становится растягивающим и достигает максимума при φ = 90  .
.
Горизонтальная составляющая меридионального усилия равна:
H=Nφ 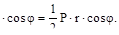
Рассмотрим пример расчёта безмоментной оболочки. Магистральный трубопровод заполнен газом, давление которого равно Р.
Здесь r1=R, r2= 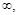 а в соответствии с ранее принятым допущением, что напряжения распределяются равномерно по толще δ оболочки
а в соответствии с ранее принятым допущением, что напряжения распределяются равномерно по толще δ оболочки
Nφ 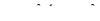 и Nθ=
и Nθ= 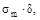
где: σm- нормальные меридиональные напряжения, а
σt- окружные (широтные, кольцевые) нормальные напряжения.
σt 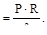
11.6 Практикум
Примеры - рассмотрены в разделе V
Вопросы для повторения
1. В каком случае изгиб называют косым?
2. Применимо ли определение “косой изгиб” для балки круглого поперечного сечения? Обоснуйте.
3. Как определяется положение нейтральной оси при косом изгибе?
4. Проходит ли нейтральная ось при косом изгибе через центр тяжести сече-ния? Обоснуйте.
5. Какие точки сечения будут опасными при косом изгибе?
6. Как определяют перемещения при косом изгибе?
7. Какие напряжения возникают в точках поперечного сечения при внецентрен-ном растяжении?
8. Проходит ли нейтральная ось при внецентренном растяжении через центр тяжести сечения? Обоснуйте.
9. Чему равно нормальное напряжение в центре тяжести сечения при внецен-тренном растяжении?
10. Могут ли при внецентренном растяжении возникать сжимающие напряже-ния в точках поперечного сечения?
11. Что называют ядром сечения?
12. Какими будут напряжения во всех точках сечения если известно, что след растягивающей силы находиться внутри ядра сечения?
13. Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?
14. Как находят опасные сечения бруса круглого сечения при изгибе с кручени-ем?
15. Какие точки круглого бруса являются опасными и какое напряженное сос-тояние в этих точках при кручении с изгибом?
16. Как выполняют проверку безопасной прочности при кручении с изгибом круглого бруса?
17. Какие допущения вводят при расчёте оболочек вращения по безмоментной теории?
18. Как определить меридиональные и окружные (широтные) нормальные нап-ряженния при расчёте тонкостенной оболочки вращения?
Тесты для повторения
В опасном поперечном сечении бруса из пластичного материала действуют Mz, My, N в напряжениях, указанных на рисунке. Какая точка будет опасной?
(а) 1; (б) 2; (в) 3; (г) 4.
 Ответ: (в), поскольку составляющие напряжения в точке 3 от каждого из изображённых внутренних факторов вызывают растягивающие напряжения.
Ответ: (в), поскольку составляющие напряжения в точке 3 от каждого из изображённых внутренних факторов вызывают растягивающие напряжения.
 2. Если на консольную балку, имеющую круглое поперечное сечение диамет-ром D действуют две взаимно перпендикулярные силы в плоскости поперечно-го сечения, а предел текучести σу извес-тен, то фактический коэффициент запа-са прочности n будет равен:
2. Если на консольную балку, имеющую круглое поперечное сечение диамет-ром D действуют две взаимно перпендикулярные силы в плоскости поперечно-го сечения, а предел текучести σу извес-тен, то фактический коэффициент запа-са прочности n будет равен:
(а) 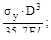 (б)
(б) 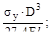
(в) 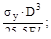 (г)
(г) 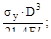
Ответ: (б). Опасным сечением будет сечение в заделке, где Mz мах=2.5F l и Mу мах=F l.
Приведённый изгибающий момент Mtot= 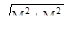 в опасном сечении равен
в опасном сечении равен 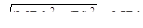
Действующие в опасной точке опасного сечения:
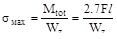
Коэффициент запаса прочности
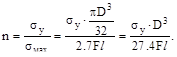
 3. Короткий стержень, имеющий прямоугольное сечение с размерами h > b, сжат силой F, приложенной в первом случае в точке А, а во втором – в точке В. Какой случай опаснее? Ответ дать сравнив возникающие нормальные напряжения
3. Короткий стержень, имеющий прямоугольное сечение с размерами h > b, сжат силой F, приложенной в первом случае в точке А, а во втором – в точке В. Какой случай опаснее? Ответ дать сравнив возникающие нормальные напряжения 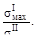 Это отношение равно:
Это отношение равно:
(а) 2.0; (б) 1.5;
(в) 1.0; (г) 0.5.
Ответ: (в), поскольку в первом случае максимальная величина
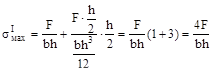 (опасные точки на линии, где приложена сила F), а во втором случае
(опасные точки на линии, где приложена сила F), а во втором случае 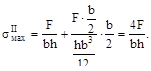
 4. Сила F действует в плоскости торцевого сечения балки. Во сколько раз воз-растут наибольшие напряжения σмах, если направление силы F отклониться от вертикального на угол α =30º? Попе-речное сечение – двутавр № 24 (Wz=298см4; Wy=34.5см4).
4. Сила F действует в плоскости торцевого сечения балки. Во сколько раз воз-растут наибольшие напряжения σмах, если направление силы F отклониться от вертикального на угол α =30º? Попе-речное сечение – двутавр № 24 (Wz=298см4; Wy=34.5см4).
(а) 2; (б) 3; (в) 4; (г) 5.
Ответ: (г), поскольку при вертикаль-ном приложении (чистый изгиб) 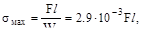 а при отклоне-
а при отклоне-
нии
силы F на 30 º (косой изгиб) 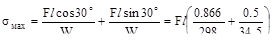 = =17.4·10-3 F l, более чем в пять раз превышает первый случай.
= =17.4·10-3 F l, более чем в пять раз превышает первый случай.
 5. Если в поперечном сечении стержня действуют два внутренних силовых фактора Mz и My, а наибольшие напряжения от каждого из них в отдельности известны (σмах(Mz) =150МПа; σмах(Mу) =80МПа), то большее суммарное напряжение равно:
5. Если в поперечном сечении стержня действуют два внутренних силовых фактора Mz и My, а наибольшие напряжения от каждого из них в отдельности известны (σмах(Mz) =150МПа; σмах(Mу) =80МПа), то большее суммарное напряжение равно:
(а) 170; (б) 190; (в) 210; (г) 230.
Ответ: (а), поскольку изгибающие моменты действу-ют во взаимно перпендикулярных плоскостях, то
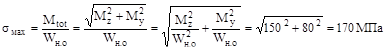 .
.
6. Если стержень из стали Ст.3 прямоугольного поперечного сечения находить-ся под действием двух сил F1 и F2, то опасной в заделке является точка:
 (а) 1; (б) 2; (в) 3; (г) 4;
(а) 1; (б) 2; (в) 3; (г) 4;
Ответ: (в) поскольку в этой точке все три внутренние силовые факторы вызывают одновременно сжатие, а материал пластич-ный.
Контрольные тесты
1. Стержень загружен двумя одинаковыми силами. Как изменится максималь-ное напряжение, если одну из сил убрать?
 (а) не изменится;
(а) не изменится;
(б) уменьшится в 2 раза;
(в) возрастёт в 1.5 раза;
(г) возрастёт в 2.5 раза.
2. Как изменится напряжение в точке А, если точку приложения силы перенести из точки А в точку В?

(а) возрастёт; (б) уменьшится;
(в) не измениться; (г) обратиться в ноль.
 3. Максимальное напряжение в стержне равно:
3. Максимальное напряжение в стержне равно:
(а) 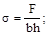 (б)
(б) 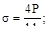
(в) 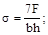 (г)
(г) 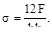
4. Допускаемое напряжение σadm. Чему равно максимальное значение силы F?

(а) 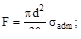 (б)
(б) 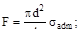
(в) 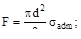 (г)
(г) 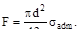
5. Как измениться максимальное напряжение в стержне, если точку прилроже-ния силы перенести в точку В?

(а) уменьшится; (б) не изменится;
(в) возрастёт; (г) станет равным 0.
6. Как изменится напряжение в точке А, если точку приложения силы перенес-ти из точки А в точку В?

(а) уменьшится; (б) не изменится;
(в) возрастёт; (г) станет равным 0.
7. Как изменится напряжение в точке А (см. рис. задачи 6), если силу перенес-ти в центр тяжести сечения?
(а) уменьшится; (б) не изменится; (в) возрастёт; (г) станет равным 0.
8. Как изменится напряжение в центре тяжести сечения стержня (точка О), если точку приложения силы (см. рис. к задаче 6) перенести из точки А в точку В?
(а) уменьшится; (б) не изменится; (в) возрастёт; (г) станет равным 0.
9. Укажите правильное положение нейтральной линии, если сила приложена параллельно оси стержня в точке А.

(а) 1-1; (б) 2-2;
(в) 3-3; (г) 4-4.
 10. На первом этапе действуют две равные силы F, параллельные оси стержня. Если на втором этапе убрать одну из сил, то максимальное напряжение σadm:
10. На первом этапе действуют две равные силы F, параллельные оси стержня. Если на втором этапе убрать одну из сил, то максимальное напряжение σadm:
(а) уменьшится на 50%;
(б) возрастёт на 50%;
(в) возрастёт на 150%;
(г) возрастёт на 250%.
11. Если к стержню приложены две силы- F и 2F, то наибольшее напряжения σмах будет равно:

(а) 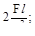 (б)
(б) 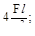
(в) 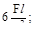 (г)
(г) 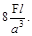

12. Вдоль оси стержня круглого поперечного сечения с квадратным отверстием в точке К (произвольной на внешнем контуре) приложена сила F=1000кН. Макси-мальное напряжение в МПа равно по модулю:
(а) 140; (б) 155;
(в) 170; (г) 185.
13. Если внецентренно приложенная сила F сжимает стержень из хрупкого материала 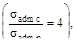 то допускаемое значение силы
то допускаемое значение силы
 F равно:
F равно:
(а) 0.14b·h·σadm p; (б) 0.17b·h·σadm p;
(в) 0.2 b·h·σadm p; (г) 0.25 b·h·σadm p.
 14. Укажите правильную эпюру σ.
14. Укажите правильную эпюру σ.
РАЗДЕЛ III. СТЕРЖНЕВЫЕ СИСТЕМЫ
12. Расчёт статически неопределимых систем методом сил
12.1 Основная система и сущность метода
Статически неопределимыми называют системы, в которых невозможно определить все реакции в связях закрепления, а также внутренние усилия в эле-ментах системы из уравнений статического равновесия. Но термин “лишние связи” является условным, поскольку при их отсутствии прочность и жёст-кость системы значительно снижается. Этот термин означает, что связи лишние только в плане превышения их количества числа независимых уравнений ра-вновесия.
Степень статической неопределимости можно определить как разность между числом искомых усилий и числом независимых уравнений равновесия, которые можно составить для рассматриваемой системы.
Для плоской системы положение жёсткого тела характеризуется тремя независимыми параметрами – двумя координатами и углом поворота, следова-тельно для равновесия на плоскости достаточно наложение трёх внешних свя-зей, что соответствует и трём независимым уравнениям равновесия. Если плос-кая система состоит из Д жёстких тел (дисков), то количество параметров, оп-ределяющих положение этой системы будет равно ЗД. Если они соединены ша-рнирами, то каждый шарнир, соединяющий две части системы, разрешая взаимный поворот, устраняет возможность взаимного смещения, т.е. уменьша-ет количество возможных перемещений системы, накладывая две дополнитель-ные связи. Каждый из опорных стержней устраняет возможность перемещения системы в соответствующем направлении. Тогда степень статической неопре-делимости, определяемую внешними связями можно подсчитать по формуле:
К=ЗД-2Ш-С,
где: Д- число частей системы, каждая из которых может рассматриваться как абсолютно жёсткое тело.
Ш- количество простых шарниров в системе, соединяющих два “диска”.
С- число опорных стержней.
Если К=0, то имеем статически определимую систему, если К<0 – статически неопределимую.
Для расчёта статически неопределимой системы дополнительно к урав-нениям статики необходимо составить К уравнений совместности перемещения в точках системы.
Для заданной системы (рис. 12.1 а)
К= 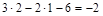
Следовательно система дважды статически неопределима, имеются две лиш-них связи. Если у заданной системы отбросить две “лишних” связи то образуем основную систему. Основная система статически определима, но при её обра-зовании необходимо обеспечить, что бы она не превратилась в механизм. Эта система может быть эквивалентна исходной, если к ней будут приложены в на-правлении отброшенных связей усилия Х1 и Х2 (рис. 12.1, б) значения которых следует определить из ограничений (совместности перемещений), которые на-кладывали отброшенные связи: 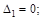
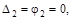 т.е. перемещения в гори-
т.е. перемещения в гори-
 зонтальном направлении правой опорной точки и угол поворота опорного сече-ния правой стойки равны нулю.
зонтальном направлении правой опорной точки и угол поворота опорного сече-ния правой стойки равны нулю.
Эти усилия рассматрива-ются как основные и дают назва-ние метода расчёта- метод сил. Определив усилия в “лишних связях”, задача оказывается ста-тически определимой. Для опре-деления перемещений следует воспользоваться универсальным методом- методом Мора, полу-чившего название по имени не-меецкого учёного, предложившего его. Рис. 12.1
12.2.Определение перемещений методом Мора
При использовании этого метода (в литературе его называют: методом возможной работы; методом фиктивной нагрузки; методом единичной нагруз-ки) необходимо рассматривать две системы нагрузок, действующих на кон-струкцию. Первая система включает все реальные нагрузки, а вторая система включает только единичную нагрузку, которая действует на конструкцию. Еди-ничная нагрузка представляет собой фиктивную или искусственно введённую нагрузку, которая позволяет определить перемещение 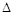 конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении ис-комого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.
конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении ис-комого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.
Действующая на конструкцию единичная нагрузка, которая представляет собой вторую систему нагрузок, вызывает возникновение реакций опор и внут-ренних усилий, которые обозначим через 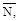
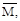
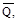
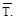 Вместе с единичной наг-рузкой и реакциями опор они образуют систему сил, которая находится в рав-новесии. Если конструкции предать малую возможную деформацию, в качест-ве которой возьмем действительные деформации конструкции, создаваемые пе-
Вместе с единичной наг-рузкой и реакциями опор они образуют систему сил, которая находится в рав-новесии. Если конструкции предать малую возможную деформацию, в качест-ве которой возьмем действительные деформации конструкции, создаваемые пе-
рвой системой нагрузок, то возможная работа внешних сил будет представлять
собой только работу, совершаемую самой единичной нагрузкой. Эта возмож-ная (виртуальная) работа равна произведению единичной нагрузки на переме-щение 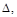 которое совершает точка её приложения; таким образом:
которое совершает точка её приложения; таким образом:
Авнш=1 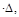
Где величина 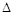 представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.
представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.
Возможная работа внутренних сил представляет собой работу, совершае-мую этими силами (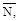
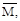
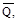
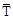 ) при возможной деформации элементов конс-трукции. Эти деформации выбираем такими же, как и действительные дефор-
) при возможной деформации элементов конс-трукции. Эти деформации выбираем такими же, как и действительные дефор-
мации, возникающие при действии на конструкцию реальных нагрузок. Обоз-начая эти деформации через 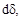
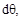
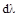 и
и 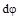 (рис. 12.2 при растяжении (а), из-гибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:
(рис. 12.2 при растяжении (а), из-гибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:
Ивнт=∫ 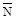
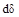 +∫
+∫ 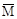
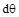 +∫
+∫ 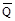
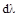 +∫
+∫ 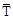
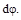
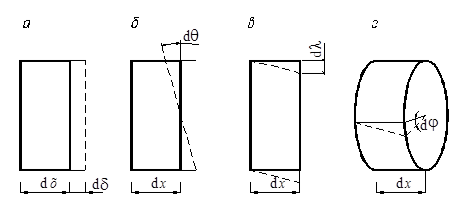
Рис. 12.2
Приравняв, выражение для работ внешних и внутренних сил получаем:
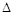 =∫
=∫ 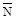
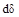 +∫
+∫ 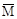
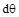 +∫
+∫ 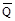
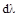 +∫
+∫ 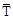
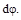
Если деформации малые упругие (справедлив закон Гука), а внутренние усилия в первой системе реальных нагрузок обозначить через NF, MF, QF и TF, то деформации элемента можно записать:
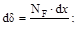
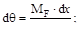
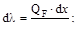
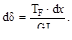
Первое из этих выражений даёт удлинения элемента при действии нормальной силы NF, а последующие деформации при изгибе, сдвиге и круче-нии.
В окончательном виде метод Мора имеет вид
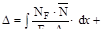
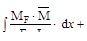
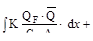
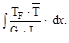
Входящий в формулу К- числовой коэффициент, зависящий от формы поперечного сечения бруса.
Порядок определения перемещений можно кратко изложить следующим образом:
1) разделив конструкцию на участки записываем аналитические выраже-ния для внутренних силовых факторов, на каждом участке, вызванных систе-мой реальных нагрузок- NF, MF, QF, TF;
2) в точке, перемещение которой хотим определить, в направлении иско-мого перемещения приложим единичную нагрузку и определяем внутренние силовые факторы, возникающие в поперечных сечениях, только от этой едини-чной нагрузки (и возникших реакций). При этом необходимо, чтобы правила знаков и направление обхода участков в п.п 1и 2 были бы те же самые.
3) подставить найденные значения в интегралы Мора и выполнить инте-грирование по всей конструкции и просуммировать результаты для получения величины перемещения 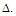 Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направле-нию единичной нагрузки.
Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направле-нию единичной нагрузки.
Не все члены интегралов Мора могут понадобиться. Так при расчёте ферм только слагаемые, содержащие нормальные силы необходимо учитывать, а для балки или плоской рамы существенными будут только деформации изги-ба и уравнение упрощается:
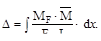
Такие интегралы можно вычислить для каждого элемента конструкции (участка), а затем просуммировать полученные результаты.
При вычислении интеграла Мора, как правило, рассматриваются такие элементы конструкций в которых жёсткости (EA, EJ, GJр) остаются постоянны-ми. Следовательно их можно вынести из под интегралов, после чего все подин-тегральные члены уравнения имеют форму произведений, скажем:
∫ МF 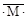 d x.
d x.
В 1925 г. студент Московского института железнодорожного транспорта А.Н. Верещагин предложил упрощение вычислений с использованием форму-лы Мора для стержневых систем, состоящих из прямых участков с постоянной (в пределах каждого участка) жёсткостью. Упрощение базируется на том, что эпюры от единичных нагрузок оказываются линейными.
Допустим, на участке длинной l нужно взять интеграл.
 J=
J= 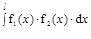
при условии, что f2(x)- линей-ная функция.
f2(x)=b+k x.
Тогда:
J= 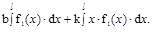
 Первый из интегралов предста-вляет собой площадь, ограни-ченную кривой f1(x) (рис. 12.3 а), которую обозначим
Первый из интегралов предста-вляет собой площадь, ограни-ченную кривой f1(x) (рис. 12.3 а), которую обозначим 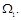 Вто-рой интеграл представляет со-бой статический момент этой площади относительно оси y, т.е.
Вто-рой интеграл представляет со-бой статический момент этой площади относительно оси y, т.е. 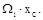
где хс - координата центра тяже-
Рис. 12.3 сти первой эпюры.
Итак, J= 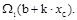 Так как b+k x c=f2(x c) (рис. 12.3 б), то
Так как b+k x c=f2(x c) (рис. 12.3 б), то
J= 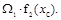
Операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

 Встречающиеся на практике эпюры могут быть расслоены на простей-шие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.
Встречающиеся на практике эпюры могут быть расслоены на простей-шие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.

Рис.12.4
Определение перемещений от симметричного и обратно симметричного воздействия надо вести раздельно, проводя вычисления только для половины
системы. Из свойства её симметрии вытекает важное правило: если при “перем-
ножении” эпюр одна из них симметрична, а другая обратно симметрична, то их “ произведение”(премещение)равно нулю.
Если жёсткость стержня переменная, то эпюру усилий от внешних воз-действий надо привести к одной жёсткости, умножая её ординаты 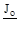 , где Jo- момент инерции одного из сечений.
, где Jo- момент инерции одного из сечений.
12.3 Канонические уравнения
Основная система с заданной нагрузкой и лишними неизвестными, экви-валентна заданной статически неопределимой системе. Следовательно, пере-мещения 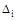 по направлению каждой неизвестных сил Х i от заданной нагрузки и всех неизвестных усилий в лишних связях должны равняться нулю.
по направлению каждой неизвестных сил Х i от заданной нагрузки и всех неизвестных усилий в лишних связях должны равняться нулю.
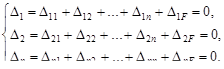
Для линейно деформируемых систем перемещение пропорционально си-ле, его вызвавшей.
Тогда:
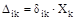
где: 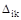 - перемещение в направлении i -той силы, вызванное к -той силой;
- перемещение в направлении i -той силы, вызванное к -той силой; 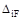 -то же от внешней нагрузки;
-то же от внешней нагрузки; 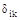 - перемещение в основной системе, соответст-вующее силе Х i при действии силы Х к =1:
- перемещение в основной системе, соответст-вующее силе Х i при действии силы Х к =1:
с учётом сказанного
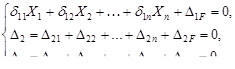
Уравнения имеют стационарную (каноническую) форму, одинаковую для всех статически неопределимых систем.
Представленная система канонических уравнений метода сил содержит главные коэффициенты при неизвестных (с одинаковыми индексами) и побочные (с разными индексами), при этом 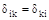 . Величины
. Величины 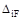 называют свободными членами канонических уравнений.
называют свободными членами канонических уравнений.
Коэффициенты при неизвестных и свободные члены уравнений опреде-ляют по интегралам Мора, а в частных случаях- по правилу Верещагина. Пред-варительно должны быть построены эпюры 
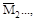
 от единичных наг-
от единичных наг-
рузок 
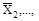
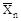 и эпюры MF от заданной нагрузки.
и эпюры MF от заданной нагрузки.
Главные коэффициенты δ ii всегда положительны. Побочные же коэффи-циенты (перемещения) δ iк могут быть положительными, отрицательными или равными нулю.
Коэффициенты и свободные члены подлежат проверке. Универсальная проверка всех коэффициентов при неизвестных состоит, в том что сумма Σδ ii + 2Σδ iк, представляющая собой условное перемещение по направлению всех не-известных от всех единичных сил 
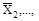
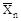 , должна быть равна величине
, должна быть равна величине
δ ss = 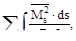
где: Ms= 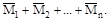
Чтобы возможные ошибки, допущенные при построении единичных эпюр, не перенесли на эпюру 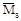 и не свести тем самым на нет всю проверку, следует строить эпюру
и не свести тем самым на нет всю проверку, следует строить эпюру 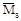 независимо от
независимо от 
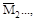
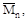 т.е. непосредственно от единичных сил
т.е. непосредственно от единичных сил 
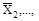
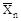 , действующих на основную систему одновре-менно.
, действующих на основную систему одновре-менно.
Если универсальная проверка приводит к недопустимо большому расхо-ждению между суммой контролируемых перемещений и условным перемеще-нием, то для нахождения ошибки можно произвести построчные проверки, ко-торые состоят в том, что сумма коэффициентов при неизвестных каждого уравнения δi1+δi2+…+δin должна быть равна величине:
δ is = 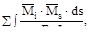
Если построчные проверки дают расхождения только в одной строке, то ошибка связана с вычислением главного коэффициента этой строки. Если же расхождения наблюдаются одновременно в двух строках, то ошибка скорее всего допущена при вычислении того побочного коэффициента, который вхо-дит в обе строки.
Проверка свободных членов уравнений состоит в том, что их сумма 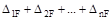 должна быть равна величине
должна быть равна величине
Δ sF = 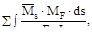
После проверки коэффициентов при неизвестных и свободных членов
канонических уравнений производят их решение и находят 
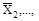
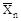 .
.
12.4 Построение эпюр внутренних усилий
Для построения эпюры моментов в статически определимой системе мо-жно использовать зависимость:
М= 
Существует так называемая кинематическая проверка, состоящая в про-верке равенства нулю условного перемещения основной, или, что то же, задан-ной системы по направлению всех неизвестных от всех неизвестных и заданной нагрузки, т.е.
Δ S = 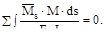
Должны выполнятся и отдельные условия:
Δ i = 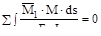 (i =1,2…,n).
(i =1,2…,n).
Эти условия называют деформационной проверкой, суть которой состоит в том, что перемножают окончательную эпюру изгибающих моментов Mz и одну из единичных эпюр изгибающих моментов Mi, определяя при этом перемещение в i -той лишней связи, зная, что оно должно быть равным нулю.
Эпюры поперечных сил Q и продольных сил N строятся для основной системы с заданной нагрузкой и вычисленными неизвестными. В то же время для построения эпюры Q можно использовать заданную нагрузку и эпюру М и рассматривать равновесие отдельных стержней. Для построения эпюры N можно использовать заданную нагрузку и эпюру Q и рассматривать равновесие узлов.
Проверка эпюр Q и N состоит в том, что для любой отсечённой части рамы суммы проекций на две оси внешних и внутренних сил должна равняться нулю (статическая проверка).
Для определения перемещения любой точки статически неопределимой
системы достаточно образовать основную систему и в точке, перемещение ко-торой необходимо определить, приложить единичную нагрузку в направлении искомого перемещения. Построив эпюру изгибающих моментов от этого воз-действия в любой основной системе, следует перемножить её с окончательной эпюрой изгибающих моментов статически неопределимой системы. Если пере-мещение получено со знаком “минус”, то действительное направление переме-щения противоположно направлению единичной нагрузки.
12.5 Практикум
Примеры 1. Определить прогиб Vс и угол поворота φс в точке С балки, считая
жёсткость сечения балки постоянной (EJz=const).
 Определяем реакции в опорах ис-пользуя симметрию расчётной схе-мы, то
Определяем реакции в опорах ис-пользуя симметрию расчётной схе-мы, то
RA=RB= 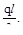
 Балка имеет два участка. На левом участке:
Балка имеет два участка. На левом участке:
 MF=RА x -
MF=RА x - 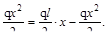
Эпюра MF представлена на (рис. б).
Для определения вертикального перемещения в точке С приложим единичную силу в вертикальном
направлении (рис. в).
 На левом участке изгибающий момент определяем рассмотрев, как и первом случае левую часть балки
На левом участке изгибающий момент определяем рассмотрев, как и первом случае левую часть балки
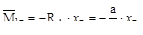
На правом участке

Подставив в интеграл Мора полученные аналитические выражения, имеем:
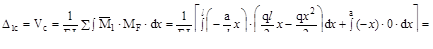
= 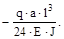
Полученное перемещение отрицательно, следовательно точка С перемес-тилась вверх (в направлении противоположном вектору единичной силы).
Для определения угла поворота в сечении С следует в этом сечении при-ложить единичную нагрузку в виде момента. На левом участке выражение для изгибающего момента от единичного имеет вид:
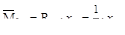
а на правом участке 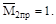
С учётом того, что MFпр=0, в интегралах Мора будет только одно слагае-мое:
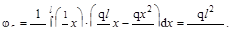
Угол поворота φс > 0, т.е. поворот совершён в направлении М2 (против хода часовой стрелки).
Воспользовавшись способом Верещагина для получения прогиба Vc не-обходимо площадь грузовой эпюры MF умножить на ординату единичной эпюры 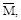 под центром тяжести параболической эпюры MF
под центром тяжести параболической эпюры MF
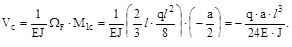
Для угла поворота φс следует перемножить MF 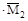
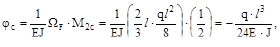
где:  и
и 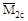 - значения первой и второй (соответственно) единичных эпюр под центром тяжести грузовой эпюры MF. Слагаемое для правого участка рав-ны нулю, поскольку MFпр =0. На рис. б, в, г, даны эпюры MF,
- значения первой и второй (соответственно) единичных эпюр под центром тяжести грузовой эпюры MF. Слагаемое для правого участка рав-ны нулю, поскольку MFпр =0. На рис. б, в, г, даны эпюры MF, 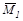 и
и 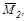 а на ри-сунке д - форма изогнутой оси балки.
а на ри-сунке д - форма изогнутой оси балки.
2. Способом Верещагина определить вертикальное перемещение сечения А и угол поворота сечения В если Е =2·105 МПа, J =2·103 см4.
Построим эпюру MF (рис. б) известным способом и представим ее «расслоенной» (рис. в) на простейшие площадки: прямоугольник с центром тяжести С1, треугольники с центром тяжести С2 и С4 и параболический сегмент высотой 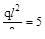 , с центром тяжести С3.
, с центром тяжести С3.
На рис. г показана эпюра 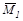 , полученная в результате нагружения еди-ничной силой F=1, приложенной в точке А и обозначены значения ηi под цент-рами тяжести каждой из простейших площадок.
, полученная в результате нагружения еди-ничной силой F=1, приложенной в точке А и обозначены значения ηi под цент-рами тяжести каждой из простейших площадок.
На рисунке д показана эпюра 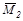 , полученная в результате нагружения
, полученная в результате нагружения
единичной парой сил М=1, приложенной в сечении В.

 Поскольку центр тяжести прямоугольника находится на расстоянии 0,5 м от точки А, то η1=
Поскольку центр тяжести прямоугольника находится на расстоянии 0,5 м от точки А, то η1= 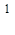 (см. рис. г). Определить значение осталь-ных η2, η3, η4 для участка ВС из уравнения
(см. рис. г). Определить значение осталь-ных η2, η3, η4 для участка ВС из уравнения 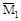 = l · х, задавая в каждом случае координаты С2, С3 и С4 в системе коор-динат, имеющих начало в край-ней левой точке или вычислив приращения ηi на участке ВС.
= l · х, задавая в каждом случае координаты С2, С3 и С4 в системе коор-динат, имеющих начало в край-ней левой точке или вычислив приращения ηi на участке ВС.



 С учетом этого опреде-лим прогиб балки в сечении А:
С учетом этого опреде-лим прогиб балки в сечении А:

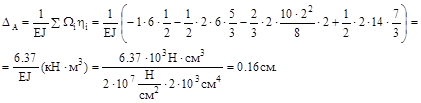
Знак “минус” в формуле ставится в том случае, когда грузовая эпюра МF и ордината единичной эпюры 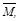 находятся по разные стороны базовой линии эпюр.
находятся по разные стороны базовой линии эпюр.
Для определения угла поворота в сечении В приложим в этом сечении единичную пару сил М=1, построим эпюру 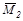 (рис. д) и перемножим МF·
(рис. д) и перемножим МF· 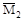 .
. 
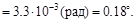
Оба значения и VA и φВ получены со знаком “плюс”, следовательно точ-ка А переместилась вниз, а сечение В повернулось против часовой стрелки (в том же направлении, что и приложенные единичные нагрузки).
Примеры раскрытия статической неопределимости рам с использованием метода сил и способа Верещагина даны в разделе V.
Вопросы для повторения
1. Что называют статически определимыми и статически неопредели-мыми системами?
2. Что называется степенью статической неопределимости системы?
3. Как определяется степень статической неопределимости?
4. Что представляет собой основная система?
5. В чём заключается выбор основной системы?
6. Что выражает каждое из канонических уравнений?
7. Каков физический смысл произведений 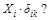
8. Какие перемещения называют главными и побочными. Какими свой-ствами они обладают?
9. В каком порядке производится расчёт статически неопределимых сис-тем?
10. Перемножением каких эпюр определяют коэффициенты и свободные члены системы канонических уравнений?
11. Как определяются значения неизвестных Хi?
12. Какими приёмами можно построить окончательную (суммарную) эпюру изгибающих моментов?
13. Как производится статическая проверка правильности раскрытия ста-тической неопределимости системы?
14. Как проводят деформационную проверку правильности построения окончательной эпюры М статически неопределимой системы?
15. Как производится определение перемещений в статически неопреде-лимых системах?
16. Какие системы называют геометрически неизменяемыми?
 Тесты для повторения
Тесты для повторения
1. Степень статической неопределимости заданной рамы равна
(а) 1; (б) 2; (в) 3; (г) 4.
Ответ: (в). Для равновесия (геометрической неиз-меняемости) достаточно трёх связей, а опоры накла-дывают шесть связей, т.е. три- избыточные (лиш-ние).
Решение можно получить и по формуле(см. 12.1)
К=ЗД-2Ш-С (*)
К= 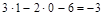 -трижды статически неопределимая система.
-трижды статически неопределимая система.
2. Степень статической неопределимости заданной рамы равна:
(а) 5; (б) 2; (в) 3; (г) 4.
 Ответ: (г). Система дважды статически нео-пределима внешне, замкнутый контур увеличи-вает на 3 степень неопределимости, а простой шарнир С- уменьшает на единицу, т.о.
Ответ: (г). Система дважды статически нео-пределима внешне, замкнутый контур увеличи-вает на 3 степень неопределимости, а простой шарнир С- уменьшает на единицу, т.о.
К=2+3-1=4.
Если провести анализ по формуле (*), то число дисков-1, простых шарниров в системе-1, число опорных стержней (внешних связей) - 5.
К= 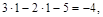
т.о. система четырежды статически неопределима.
 3. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
3. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
Ответ: (г), поскольку система представляет в этом
 случае “мгновенный механизм” (не может противодействовать повороту относительно левого шарнира).
случае “мгновенный механизм” (не может противодействовать повороту относительно левого шарнира).

 4. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
4. Укажите неправильный вариант основной системы для заданной статически неопределимой рамы.
Ответ: (г) поскольку данная система - механизм может перемещаться в горизонтальной плоскости.

 5. Задана статически неопределимая балка (рис. а), принята её эквивалентная система (рис. б), построены грузовая МF и единичная
5. Задана статически неопределимая балка (рис. а), принята её эквивалентная система (рис. б), построены грузовая МF и единичная 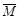 эпюры изгибающих мо-ментов в основной системе. Чему равно значение Х1?
эпюры изгибающих мо-ментов в основной системе. Чему равно значение Х1?
(а) 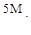 (б)
(б) 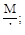 (в)
(в) 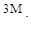 (г)
(г) 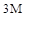
Ответ: (а). Каноническое уравнение метода сил для один раз статически неопределимой системы
δ11Х1+∆1F=0.
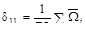 ·
· 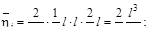
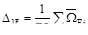
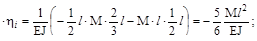
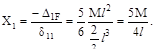
6. Задана статически неопределимая балка, построена её окончательная эпюра М изгибающих моментов. Укажите изогнутую ось балки.



Ответ: (в), поскольку только у этой изогнутой оси нет поворота сечения в за-делке и на левой части выпуклость “вверх” соответствует зоне растянутых “во-локон” на эпюре, а правая часть эпюры свидетельствует о том, что растянуты нижние “волокна”.
Контрольные тесты
1.Укажите пару коэффициентов канонических уравнений, равных между собой:
(а) δ11 и δ12; (б) δ23 и δ32; (в) δ22 и δ33; (г) δ31 и δ23.
2. Коэффициенты канонических уравнений δik (i 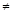 k) могут быть:
k) могут быть:
(а) δik >0; (б) δik < 0; (в) δik ≥0; (г) δik> = < 0.
3. Степень статической неопределимости заданной рамы равна:

(а) 4; (б) 3;
(в) 2; (г) 1.
 4. Степень статической неопределимости заданных рам равна (установите соот-ветствие)
4. Степень статической неопределимости заданных рам равна (установите соот-ветствие)

(д) 4; (е) 5; (ж) 6; (з) 7.
 5. Укажите неправильный вариант основной систе-мы для заданной статически неопределимой рамы.
5. Укажите неправильный вариант основной систе-мы для заданной статически неопределимой рамы.


6. Укажите правильный вариант основной системы для заданной статически неопределимой рамы.



7. Чему равен прогиб в точке А?
 (а)
(а) 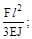 (б)
(б) 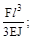
(в) 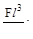 (г)
(г) 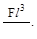
8. Количество канонических уравнений равно числу:
(а) внешних лишних связей системы;
(б) внутренних (взаимных) лишних связей системы;
(в) внешних и внутренних лишних связей системы;
(г) независимых уравнений статики для заданной системы.
9. Для статически неопределимой балки (рис. а) выбрана эквивалентная система (рис. б). Чему равно усилие Х1?

(а) 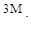 (б)
(б) 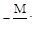
(в) 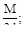 (г)
(г) 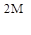

10. Для статичес<
 2020-07-12
2020-07-12 622
622








