Идея метода:
Найдем середину отрезка [ a, b ]: c= (a+b) /2. Корень остался на одной из частей: [ a, c ] или [ c, b ]. Если f (a) * f (с) <0, токорень попал на отрезок [ a, c ], тогда деление отрезка можно повторить, приняв в качестве нового правого конца точку c, т.е. b=c. В противном случае корень попал на половину [ c, b ], и необходимо изменить значение левого конца отрезка: a=c. Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности: | b – a|<ε Найдем первый корень уравнения f(x)=x3 - 6x2+3x+11=0 с точностью 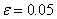
Вычисления оформляются в виде таблицы
| k | a | b | c | f(a) | f(c) | |b-a| |
| 0 | -2 | -1 | -1.5 | -27 | -10.375 | 1 |
| 1 | -1.5 | -1 | -1.25 | -10.375 | -4.07813 | 0.5 |
| 2 | -1.25 | -1 | -1.125 | -4.07813 | -1.39258 | 0.25 |
| 3 | -1.125 | -1 | -1.0625 | -1.39258 | -0.1604 | 0.125 |
| 4 | -1.0625 | -1 | -1.03125 | -0.1604 | 0.42868 | 0.0625 |
| 5 | -1.0625 | -1.03125 | -1.04688 | -0.1604 | 0.136372 | 0.03125 |
| 6 | .......... | |||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | -1.05469 | -1.05371 | -1.0542 | -0.01146 | -0.00218 | 0.000977 |
где a0, b0 - начальные границы интервала изоляции корня; 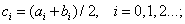
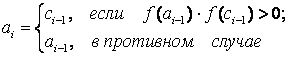
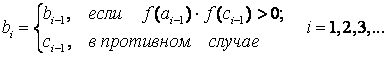
В результате расчета приближенное значение первого корня: 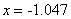 при точности
при точности 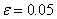 и х=-1.0542 при точности
и х=-1.0542 при точности 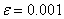 .
.
Графическая иллюстрация метода:
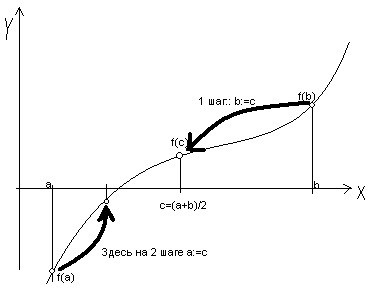
Метод простой итерации
С помощью эквивалентных преобразований приведем исходное уравнение f(x) к виду, удобному для применения метода простой итерации: x=φ (x). Выберем начальное приближение x0 ∈[ a, b ]. Следующие итерации находим по формуле: xk +1= φ (xk), т.е. x 1= φ (x0), x2 = φ (x1) и т.д.. Итерационный процесс заканчивается, если | xk+1 – xk |< ε. Представить исходное уравнение в эквивалентном виде x=φ (x) можно бесконечным числом способов. Из всевозможных таких представлений выбирают тот, который дает сходящуюся к корню последовательность вычислений. Очевидно, что 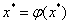 .
.
Достаточное условие сходимости: пусть φ (x) имеет производную на отрезке [a,b], 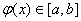 и
и 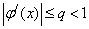 для всех x из отрезка [a,b], тогда итерационный процесс сходится к корню уравнения т.е.
для всех x из отрезка [a,b], тогда итерационный процесс сходится к корню уравнения т.е. 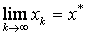 .
.
Доказательство следует из следующих оценок:
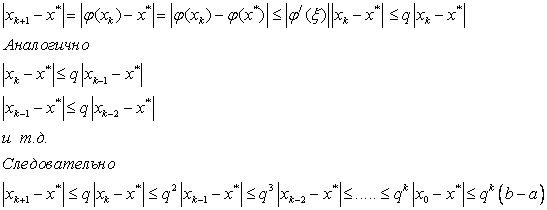
Первое неравенство следует из теоремы Лагранжа о среднем и того, что 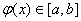 .
.
Остальные по инерции.
Так как 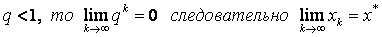 .
.
 2020-06-29
2020-06-29 201
201








