Напомним, что мы решаем уравнение f(x)=0.
Метод определяется формулой

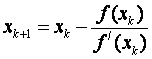
Геометрическая интерпретация такова: участок кривой y=f(x) при 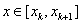 , если
, если 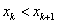 , или
, или  , если
, если 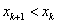 , заменяется отрезком касательной, проведённой из точки xk.
, заменяется отрезком касательной, проведённой из точки xk.
Уравнение касательной имеет вид 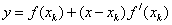 . Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:
. Найдем точку пересечения, которую обозначим xk+1, касательной с осью y=0:  .
.
Откуда  .
.
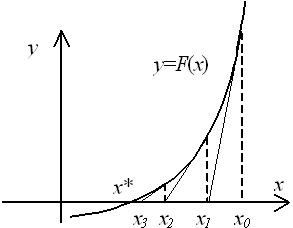
Можно показать, что | xk+ 1– x* | < q * | xk – x* |2, т.е. метод сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации при 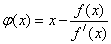 .
.
Замечание. Если известен интервал изоляции корня уравнения, в котором f//(x) не меняет знак, то в качестве начального приближения берут тот конец интервала изоляции, для которого знаки f(x) и f//(x) совпадают.
Найдем, третий корень методом Ньютона нашего исходного уравнения x3‑ 6x2+3x+11=0, который лежит на интервале [4, 5] с точностью 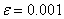 . Сначала убедимся, что f//(x) не меняет знака на этом отрезке.
. Сначала убедимся, что f//(x) не меняет знака на этом отрезке.
f//(x)=6x-12. f//(x)>0 при x>2, т.е. f//(x)>0 на интервале [4,5]. Так как f(5)=1>0, то x0=5.
Вычисления оформим в виде таблицы:
| k | xk | |xk+1-xk| | f(xk) | f/(xk) |
| 0 | 5 | - | 1 | 18 |
| 1 | 4.944444 | 0.055556 | 0.027606 | 17.00926 |
| 2 | 4.942821 | 0.001623 | 2.33E-05 | 16.98059 |
| 3 | 4.94282 | 1.37E-06 | 1.66E-11 | 16.98057 |
Здесь f(xk)=xk3‑ 6xk2+3xk+11, f/(xk)=3xk-12xk+3,  .
.
В качестве корня можно взять значение: x=4.943. Видно, что процесс сошелся уже на второй итерации.
Для сравнения найдем первый корень нашего уравнения x3‑ 6x2+3x+11=0 на отрезке [-2,-1] методом Ньютона:
Так как f//(x)=6x-12, то f//(x)<0 на интервале [-2,-1], а так как f(-2)=-27>0, то x0=-2.
| k | xk | |xk+1-xk| | f(xk) | f/(xk) |
| 0 | -2 | -27 | 39 | |
| 1 | -1.30769 | 0.692308 | -5.41966 | 23.82249 |
| 2 | -1.08019 | 0.227502 | -0.50182 | 19.46272 |
| 3 | -1.05441 | 0.025783 | -0.00613 | 18.9882 |
| 4 | -1.05408 | 0.000323 | -9.5E-07 | 18.98229 |
| 5 | -1.05408 | 5.02E-08 | -2.3E-14 | 18.98229 |
Напомним, что методом дихотомии мы достигли данной точности 0.001 на 10-ой итерации.
Вычислим второй корень нашего уравнения на отрезке [1,3]. Заметим, что f//(x)=6x-12 меняет знак на отрезке при х=2. Уменьшим интервал изоляции так, чтобы f//(x) не меняла знака. Рассмотрим интервал [2.1; 3]. f//(2.1)=6*2.1-12=0.6>0 b f(2.1)=0.101>0. Следовательно, x0=2.1.
| k | xk | |xk+1-xk| | f(xk) | f/(xk) |
| 0 | 2.1 | 0.101 | -8.97 | |
| 1 | 2.11126 | 0.01126 | 3.95E-05 | -8.96286 |
| 2 | 2.111264 | 4.4E-06 | 6.47E-12 | -8.96286 |
| 3 | 2.111264 | 7.22E-13 | 0 | -8.96286 |
Если сравнивать с методом простой итерации, то значение этого корня мы получили за две итерации вместо шести.
Эти примеры показывают, что метод Ньютона является более быстросходящимся. Но для его использования необходимо брать начальное приближение достаточно близким к корню.
Упрощенный метод Ньютона. Эта модификация метода Ньютона используется, если производная f / (x)представляет собой сложную функцию, и для ее вычисления на каждой итерации используется много времени. Зададим x0 – начальное приближение и вычислим производную z=f / (x0). На следующих итерациях используется вычисленное значение производной: 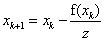 . Это упрощение несколько замедляет процесс сходимости к решению, однако сокращает время каждого итерационного цикла.
. Это упрощение несколько замедляет процесс сходимости к решению, однако сокращает время каждого итерационного цикла.
Метод хорд
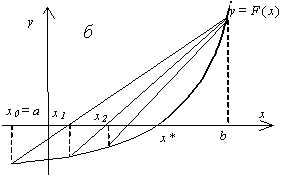
В этом методе кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f //(a) метод хорд имеет два варианта, изображенных на рис. 2 а, б.
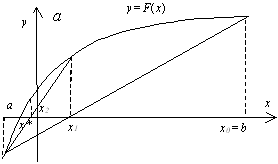
| 
|
| Рис. 2. Метод хорд для F (a) F // (a) > 0(а) и F (a) F // (a) < 0(б) | |
Пусть f(a)f //(a)>0 (рис. 2 а). Тогда x0=b, точка a будет оставаться неподвижной. Следующее приближение x1 находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x0, f(x0)) с осью x. Уравнение хорды: 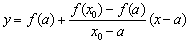 . Тогда точка пересечения хорды с осью x:
. Тогда точка пересечения хорды с осью x: 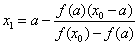 .
.
Пусть теперь f(a)f //(a)<0 (рис. 2). Тогда x0=a, точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x0, f(x0)):  . Вычисляем точку пересечения хорды с осью x:
. Вычисляем точку пересечения хорды с осью x: 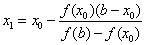 .
.
На следующей итерации в качестве x0 надо взять вычисленное значение x1.
Т аким образом, имеем следующую последовательность вычислений:
Если f(a) f //(a)>0, то x0=b и 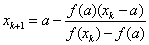 .
.
Если же f(a) f //(a)<0, то x0=a и 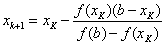 .
.
Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: | f (x1)| < ε или 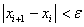 .
.
 2020-06-29
2020-06-29 68
68







