Пусть u – компактное множество, а g 1,…, gm – непрерывные функции,  .
.
Теорема (Гермейер). Пусть u 0 – эффективная точка, причем gi (u 0)>0 для всех i= 1,…, m. Тогда существуют положительные числа l1,…l m такие, что  и x 0 является точкой максимума функции
и x 0 является точкой максимума функции  .
.
Доказательство. Положим 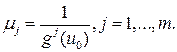 Тогда
Тогда  Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, migi (u)£1. значит,
Пусть u – любая точка. Так как точка u 0 – эффективна, найдется номер i, для которого gi (u)£ gi (u 0), или, что то же самое, migi (u)£1. значит,  а это означает, что u 0 – одна из точек максимума функции
а это означает, что u 0 – одна из точек максимума функции  .
.
Остается положить  и заметить, что тогда u 0 – одна из точек максимума функции f (u). Теорема доказана.
и заметить, что тогда u 0 – одна из точек максимума функции f (u). Теорема доказана.
К сожалению, нельзя утверждать, что всякая точка максимума функции  будет эффективной точкой многокритериальной задачи.
будет эффективной точкой многокритериальной задачи.
Пример.Пусть u ={(u 1, u 2): 0£ u 1£1, 0£ u 2£1}, g 1(u)= u 1, g 2(u)= u 2. при  точки максимума функции
точки максимума функции  образуют отрезок {(u 1, u 2): u 1=1, 0.5£ u 2£1}, но только одна его точка (1,1) является эффективной.
образуют отрезок {(u 1, u 2): u 1=1, 0.5£ u 2£1}, но только одна его точка (1,1) является эффективной.
Теорема.Пусть существуют такие положительные числа  что
что  и x 0 является точкой максимума функции
и x 0 является точкой максимума функции  . тогда точка x 0 является слабо эффективной.
. тогда точка x 0 является слабо эффективной.
Доказательство. Допустим противное. Тогда найдется такая точка u 1, что 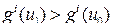 для всех i =1,…, m. но тогда
для всех i =1,…, m. но тогда  что противоречит условию.
что противоречит условию.
Пусть теперь множество u выпукло, а функции g 1,…, gm вогнуты.
Теорема (Карлин).Пусть x 0 – эффективная точка. Тогда существуют неотрицательные числа p 1,…, p m такие, что  и x 0 является точкой максимума функции
и x 0 является точкой максимума функции 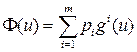 .
.
Доказательство. Не ограничивая общности, можем считать, что gi (u)>0 для всех i= 1,…, m. В силу теоремы Гермейера существуют положительные числа  для которых u 0 реализует максимум функции
для которых u 0 реализует максимум функции  .
.
Тогда (u 0 ,f (u 0)) является решением задачи математического программирования
 ,
, 
В силу теоремы Куна–Такера найдутся такие неотрицательные числа a i, i= 1,…, m, для которых (u 0 ,f (u 0)) будет точкой максимума функции

на множестве  , но это возможно, только если
, но это возможно, только если
 , (30)
, (30)
а тогда u 0 является точкой максимума функции  .
.
Остается заметить, что в силу равенства (30), по крайней мере, одно ai не равно нулю. Тогда мы можем положить  .
.
Теорема. Пусть существуют положительные числа p 1,…, p m такие, что  и u 0 является точкой максимума функции
и u 0 является точкой максимума функции 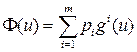 . тогда точка u 0 является эффективной.
. тогда точка u 0 является эффективной.
Доказательство. Допустим противное. Тогда найдется такая точка u 1, что gi (u 1)³ gi (u 0) для всех i =1,…, m, причем, по крайней мере, одно из этих неравенств не обращается в равенство. Умножая эти неравенства на pi и суммируя, получим неравенство F(u 1)>F(u 0), что противоречит условию.
Нельзя утверждать, что всякая эффективная точка может быть найдена в результате максимизации функции 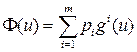 с положительными коэффициентами p 1,…, p m.
с положительными коэффициентами p 1,…, p m.
Пример. Пусть  ,
,  . Максимум функции
. Максимум функции  достигается в точке
достигается в точке  . в то же время, точка (1, 0) является эффективной.
. в то же время, точка (1, 0) является эффективной.
С другой стороны, при неотрицательных коэффициентах p 1,…, pm, точка максимума функции 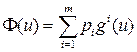 может быть неэффективной в многокритериальной задаче.
может быть неэффективной в многокритериальной задаче.
Пример. Пусть  Точки максимума функции F(u)=1× g 1(u)+0× g 2(u) образуют отрезок {(u 1, u 2): u 1=1, 0£ u 2£1}, а эффективной является только одна точка (1,1) этого отрезка.
Точки максимума функции F(u)=1× g 1(u)+0× g 2(u) образуют отрезок {(u 1, u 2): u 1=1, 0£ u 2£1}, а эффективной является только одна точка (1,1) этого отрезка.
Теорема. Пусть существуют неотрицательные числа p 1,…, p m такие, что  и u 0 является точкой максимума функции
и u 0 является точкой максимума функции 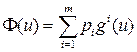 . тогда точка u 0 является слабо эффективной.
. тогда точка u 0 является слабо эффективной.
Доказательство. Допустим противное. тогда найдется такая точка u 1, что 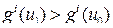 для всех i =1,…, m. Умножая эти неравенства на pi и суммируя, получим неравенство
для всех i =1,…, m. Умножая эти неравенства на pi и суммируя, получим неравенство  что противоречит условию.
что противоречит условию.
Примеры
Пример. Пусть множество u представляет собой стандартный симплекс u ={(u 1, u 2, u 3): u 1³0, u 2³0, u 3³0, u 1+ u 2+ u 3=1} и имеется два критерия g 1(u)=2 u 1+7 u 2+ u 3 и g 2(u)=3 u 1+ u 2+4 u 3.
Найдем точки максимума функции F(u)= pg 1(u)+(1– p) g 2(u). Так как критерии в данной задаче линейны, а максимум линейной функции непременно достигается в одной из вершин, то  . Нарисовав графики, нетрудно понять, что при 0£ p £1/3 максимум достигается в вершине (0,1,0), а при 1/3£ p £1 он достигается в вершине (0,0,1). При p =1/3 точки максимума заполняют все ребро, соединяющие эти вершины. Таким образом, все точки этого ребра являются эффективными.
. Нарисовав графики, нетрудно понять, что при 0£ p £1/3 максимум достигается в вершине (0,1,0), а при 1/3£ p £1 он достигается в вершине (0,0,1). При p =1/3 точки максимума заполняют все ребро, соединяющие эти вершины. Таким образом, все точки этого ребра являются эффективными.
Пример. Пусть множество u представляет собой стандартный симплекс u ={(u 1, u 2, u 3): u 1³0, u 2³0, u 3³0, u 1+ u 2+ u 3=1} и имеется два критерия g 1(u)=3 u 1+7 u 2+ u 3 и g 2(u)=4 u 1+ u 2+4 u 3.
Анализ показывает, что в данном случае эффективными являются все точки, лежащие на двух ребрах: соединяющем вершину (1,0,0) с вершиной (0,1,0) и соединяющем вершины (1,0,0) и (0,0,1). В этом случае множество эффективных точек не выпукло.
В двух предыдущих примерах полезно нарисовать образ множества u в пространстве критериев.
Пример: дуополия Курно. Две фирмы выпускают однородный товар и продают его на рынке. Цена, складывающаяся на рынке, линейно убывает с ростом суммарного предложения: p (u) =a–b (u 1+ u 2), где u 1 и u 2 объемы выпуска продукции первой и второй фирмой соответственно (по своему смыслу величины u 1 и u 2 неотрицательны). Пусть затраты первой и второй фирм на выпуск единицы продукции равны c 1 и c 2, а их цели состоят в максимизации прибылей g 1(u 1, u 2)= p (u) u 1– c 1 u 1 и g 2(u 1, u 2)= p (u) u 2– c 2 u 2. Найдем эффективные точки в этой двухкритериальной задаче.
Для этого найдем максимум функции F(u 1, u 2)= tg 1(u 1, u 2) + (1– t) g 2(u 1, u 2). Имеем  . При фиксированном управлении одной фирмы эта функция представляет собой квадратный трехчлен относительно управления другой фирмы с отрицательным старшим коэффициентом. Поэтому, максимум этой функции достигается в критической точке тогда и только тогда, когда последняя лежит внутри области u 1³0, u 2³0. В противном случае максимум находится на границе этой области.
. При фиксированном управлении одной фирмы эта функция представляет собой квадратный трехчлен относительно управления другой фирмы с отрицательным старшим коэффициентом. Поэтому, максимум этой функции достигается в критической точке тогда и только тогда, когда последняя лежит внутри области u 1³0, u 2³0. В противном случае максимум находится на границе этой области.
Критическая точка есть решение системы уравнений

Решая эту систему относительно u 1 и u 2, получим параметрическое представление

множества эффективных точек.
Исключив же из этой системы параметр p, получим уравнение
 множества эффективных точек. Нетрудно видеть, что это уравнение параболы с осью, параллельной биссектрисе координатных углов. Пересечение этой параболы с неотрицательным квадрантом и дает множество эффективных точек. Поскольку это множество пересекается с любым лучом, выходящим из начала координат и лежащим в неотрицательном квадранте, других эффективных точек нет.
множества эффективных точек. Нетрудно видеть, что это уравнение параболы с осью, параллельной биссектрисе координатных углов. Пересечение этой параболы с неотрицательным квадрантом и дает множество эффективных точек. Поскольку это множество пересекается с любым лучом, выходящим из начала координат и лежащим в неотрицательном квадранте, других эффективных точек нет.
ЗАДАЧИ
1. Мнение ученого совета по любому вопросу складывается из мнений каждого из m его членов по правилу большинства голосов. Выразите соответствующую свертку через элементарные операции, если число членов совета нечетно.
2. Мнение ученого совета по любому вопросу складывается из мнений каждого из m его членов по правилу большинства голосов. Выразите соответствующую свертку через элементарные операции, если число членов совета четно и в случае равенства голосов решающим является мнение председателя совета.
3. Студенту за сессию предстоит сдать пять экзаменов, на каждом из которых он может получить оценку от 2 до 5. Для получения стипендии необходима сдать все экзамена как минимум на удовлетворительно, и при этом получить не более одной тройки. Выразите соответствующую свертку критериев через элементарные операции.
4. В биатлонной гонке принимают участие 7 спортсменов от каждой страны. По ее итогам каждый из них получает целое число очков от 0 до 30. в командный зачет идет сумма результатов трех лучших гонщиков. Выразите соответствующую свертку критериев через элементарные операции.
5. В каждой гонке, входящей в зачет кубка мира спортсмен получает целое число очков от 0 до 50. В общий зачет идет сумма очков, набранных в 30 гонках, за исключением трех худших. Выразите соответствующую свертку критериев через элементарные операции.
6. В командной гонке конькобежцев принимают участие три спортсмена. Результат команды равен времени третьего из финишировавших. Выразите соответствующую свертку критериев через элементарные операции (время измеряется с точностью до сотых долей секунды).
7. Качество прыжка в соревнованиях по прыжкам с трамплина оценивают пять арбитров. Каждый из них выставляет оценку от 0 до 20 баллов с шагом 0.5 балла. Самая высокая и самая низкая оценка отбрасываются, а сумма трех оставшихся идет в зачет соревнования. Выразите соответствующую свертку критериев через элементарные операции.
8. Пусть u – компактное множество, а g 1,…, gm – непрерывные функции, gi: u ®  . Докажите, что для любой неэффективной точки u 0 найдется доминирующая ее эффективная точка u 1.
. Докажите, что для любой неэффективной точки u 0 найдется доминирующая ее эффективная точка u 1.
9. Докажите, что множество всех эффективных векторов из выпуклого компакта в  является компактом.
является компактом.
10. Постройте пример выпуклого компакта в  3, для которого множество эффективных векторов не замкнуто.
3, для которого множество эффективных векторов не замкнуто.
11. Докажите, что множество слабо эффективных стратегий совпадает с множеством решений уравнения 
12. Докажите, что множество эффективных стратегий совпадает с множеством решений системы неравенств  , где
, где 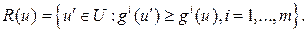
13. Докажите, что если множество u компактно, а функции gi непрерывны, то найдется такой вектор b, что множество слабо эффективных стратегий равно  , где
, где  , а объединение берется по всем векторам r с положительными компонентами.
, а объединение берется по всем векторам r с положительными компонентами.
14. Докажите, что если множество u компактно, а функции gi непрерывны, то найдется такой вектор b, что множество эффективных стратегий равно  , где
, где  , множество d (r,b) определено так же, как в предыдущей задаче, а объединение берется по всем векторам r с положительными компонентами.
, множество d (r,b) определено так же, как в предыдущей задаче, а объединение берется по всем векторам r с положительными компонентами.
15. Пусть множество u представляет собой стандартный симплекс u ={(u 1, u 2, u 3): u 1³0, u 2³0, u 3³0, u 1+ u 2+ u 3=1} и имеется два критерия  и
и 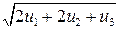 . Найдите множество эффективных точек.
. Найдите множество эффективных точек.
16. Пусть в игре n лиц ui =[0,¥),  , где a,b,ci – положительные числа. Найдите ситуации, оптимальные по Парето.
, где a,b,ci – положительные числа. Найдите ситуации, оптимальные по Парето.
17. Пусть в игре n лиц ui =[0,¥),  (считаем, что 0/0=0), где ai,bi – положительные константы. Найдите ситуации, оптимальные по Парето.
(считаем, что 0/0=0), где ai,bi – положительные константы. Найдите ситуации, оптимальные по Парето.
18. Пусть u ={(u 1,…, um): ui ³0, u 1+…+ u n= a }, v ={(v 1,…, vm): vi ³0, v 1+…+ v n= b },  ,
,  . Найдите ситуации, оптимальные по Парето (pi,qi,ai,bi – неотрицательные, a,b – положительные числа).
. Найдите ситуации, оптимальные по Парето (pi,qi,ai,bi – неотрицательные, a,b – положительные числа).
19. Пусть u ={(u 1,…, um): ui ³0, u 1+…+ u n= a }, v ={(v 1,…, vm): vi ³0, v 1+…+ vn = b },  (ai,bi – неотрицательные, pi,qi a,b – положительные числа). найдите ситуации, оптимальные по Парето.
(ai,bi – неотрицательные, pi,qi a,b – положительные числа). найдите ситуации, оптимальные по Парето.
20. Пусть ui =[0, ai ],  , где ci – положительные константы. Существуют ли в этой игре ситуации, оптимальные по Парето?
, где ci – положительные константы. Существуют ли в этой игре ситуации, оптимальные по Парето?
21. Пусть ui =[0,¥),  , где ci – положительные константы. Существуют ли в этой игре ситуации, оптимальные по Парето.
, где ci – положительные константы. Существуют ли в этой игре ситуации, оптимальные по Парето.
22. Пусть a,b,c – положительные константы, u=v =(0,¥), g 1(u,v)= u (a–bu+cv), g 2(u,v)= v (a–bv+cu). найдите ситуации, оптимальные по Парето.
23. Пусть в игре n лиц ui ={0,1}, 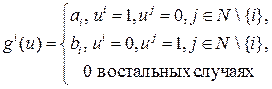 где ai,bi – положительные константы. найдите ситуации, оптимальные по Парето.
где ai,bi – положительные константы. найдите ситуации, оптимальные по Парето.
 2020-07-12
2020-07-12 300
300








