Нелинейное программирование

Нелинейное программирование – раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. К нелинейному программированию относят квадратичное, дробное, выпуклое, дискретное, целочисленное и геометрическое программирование.

В общем виде задачу нелинейного программирования можно сформулировать так:

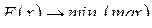                                       (31)

при условии

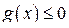,                                            (32)

где х – вектор искомых переменных;

F (х) - целевая числовая функция;

g (x) – вектор-функция системы ограничений.

При этом могут быть разные случаи:

1) целевая функция – нелинейная, а ограничения – линейны;

2) целевая функция – линейная, а ограничения (хотя бы одно из них) – нелинейные;

3) целевая функция и ограничения нелинейные.

Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях (32) имеют место:

а) знаки равенства;

б) знаки неравенства.

Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.

При решении некоторых нелинейных задач иногда удается использовать линейную теорию. Для этого вводят допущение, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению переменных. Такой подход называется методом кусочно-линейных приближений.

Среди большого числа вычислительных алгоритмов нелинейного программирования значительное место занимают:

- различные варианты градиентных методов (метод проекции градиента, метод условного градиента и т. п.);

- методы штрафных функций;

- методы барьерных функций;

- метод модифицированных функций Лагранжа и др.

Нелинейные задачи с ограничениями в форме равенств нередко решаются с помощью введения функции Лагранжа:

где L (x, λ) - лагранжиан;

φ(x) - целевая функция;

λ _i (i = 1, 2,..., k) – множители Лагранжа;

k - число ограничений g_i (x).

Универсального метода, позволяющего находить наиболее эффективным способом решение любой нелинейной задачи, не существует. Поэтому для каждой конкретной задачи, учитывая ее специфику, подбирают тот или иной наиболее подходящий метод (и алгоритм) решения.

Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров. Хорошо известно, что чем больше партия закупаемого товара, тем меньше стоимость единицы продукта. Каждому знакомо понятие розничных и оптовых цен.

 

Метод Фибоначчи

Этот метод является более эффективным по сходимости, чем метод дихотомии, и обладает наибольшей скоростью сходимости для класса непрерывных функций. В нем, как и в методе «золотого сечения», на каждом шаге производится только одно определение целевой функции, а в методе дихотомии два. Но в этом методе требуется заранее выбрать число испытаний N.

Метод основан на использовании чисел Фибоначчи для нахождения точек, в которых определяется целевая функция F (х).

Числа Фибоначчи образуют последовательность целых чисел так, что 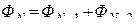  при .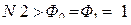

Первые 15 чисел Фибоначчи.

N	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
ФN	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610

В основу схемы поиска экстремума положены два исходных соотношения

L_{N -2} = L_{N -1} + L_N, при N 3, и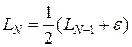

Первое из них связывает длины трех соседних (по номерам) интервалов неопределенности. Второе требует, чтобы процесс поиска экстремума всегда завершался одинаково: симметричным размещением двух последних точек (х_{N -1} и х_N) на интервале L_{N -1}.

Координаты точек, в которых определяются целевые функции, находятся по формулам:

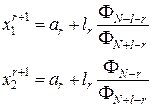
где r – номер шага (r = 0, 1, 2, 3, …, N –3);

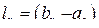   – длина интервала неопределенности на r -ом шаге;

a_r, b_r – начало и конец r -го интервала неопределенности.

Алгоритм метода является итерационной процедурой, включающей следующие этапы.

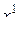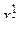На первом этапе, который соответствует первому шагу поиска () симметрично от концов начального интервала неопределенности (а и b) проводится пара испытаний в точках  и , определяемых N -ом и (N –1) числами Фибоначчи. Получаем

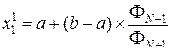
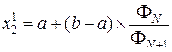
В этих точках определяется целевая функция и в зависимости от ее значений выбирается новый (суженный) интервал неопределенности.

Второй этап включает в себя (N –3) итерационных шагов. На каждом r -ом шаге в интервале неопределенности l_r, полученном на предыдущем шаге, рассматривается новая пара испытаний .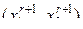

Особенностью данного алгоритма поисковой оптимизации является то, что из двух точек 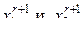, рассматриваемых на (r +1)-м шаге, одна всегда будет совпадать с одной из точек предыдущего шага 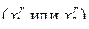, в которой уже было проведено испытание.

Третий этап характерен тем, что после проведения (N –1)-го испытания необходимо решить, по какую сторону от точки х, находящейся внутри интервала неопределенности l_{N -1}, лежит точка истинного экстремума. Для этого последнее N -е испытание проводится вблизи от точки предыдущего испытания в точке (х) или (e – х), что позволяет определить апостериорный (послеопытный) интервал неопределенностиe + l_N.

На рис. 10 приведена схема поиска экстремума по методу Фибоначчи (второй и третий этапы).

В заключение данного раздела проведем сравнение методов «золотого сечения» и Фибоначчи.

Метод Фибоначчи более эффективен по сходимости, т.е. по достижению необходимого сужения интервала неопределенности при одинаковом числе определений целевой функции.

Но его недостатки:

1. Заранее заданное число испытаний, которое нельзя менять в процессе сужения интервала неопределенности, и если после N испытаний не получена нужная точность определения оптимума, то все приходится начинать сначала, задавшись большим N.

2. При применении ЭВМ необходимо запоминать (или каждый раз вычислять) числа Фибоначчи.

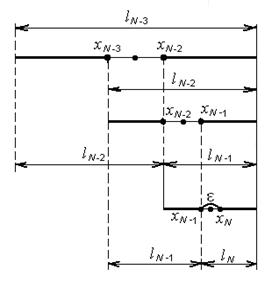
Рисунок 10.

Метод «золотого сечения» не требует заранее заданного числа испытаний. Для него требуется сравнительно небольшой объем памяти ЭВМ, и он прост в реализации.

С точки зрения эффективности метод «золотого сечения» занимает промежуточное положение между методами дихотомии и Фибоначчи.

На практике иногда комбинируют оба метода: первые шаги делают по методу «золотого сечения», а затем, когда оптимум достаточно близок, фиксируют число N и переходят к методу Фибоначчи.

СПИСОК ЛИТЕРАТУРЫ

    1. Аоки М. Введение в методы оптимизации / М. Аоки - М.: Наука, 2017. - 334 с.

    2. Ашманов С.А. Линейное программирование. Учебное пособие / С.А. Ашманов - М.: Наука, 1981. - 340 с.

    3. Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. / Б. Банди - М.: Радио и связь,2008. - 128с.

    4. Васильев Ф.П. Численные методы решения экстремальных задач. Учебное пособие / Ф.П. Васильев - М.: Наука, 1958. - 549 с.

    5. Дегтярев Ю.И. Методы оптимизации: Учебное пособие для вузов / Ю.И. Дегтярев - М.: Сов. Радио, 1980. - 272 с.

    6. Карманов В.Г. Математическое программирование. Учебное пособие / В.Г. Карманов - М.: Наука, 2016. - 285 с.

    7. Моисеев Н.Н. Методы оптимизации. Учебное пособие / Н.Н. Моисеев, Ю.П. Иванилов, Е.М. Столярова - М.: Наука, 2018. - 351 с.

    8. Моисеев Н.М. Методы оптимизации / Н.М. Моисеев - М.: Наука, 1978. - 351с.

    9. Поляк Б. Т. Введение в оптимизацию / Б. Т. Поляк - М.: Наука, 1983 - 384 с.

    10. Понтрягин Л.С. Математическая теория оптимальных процессов / Л.С. Понтрягин - М.: Наука, 1983. - 392 с.

    11. Сухарев А.Г. Курс методов оптимизации / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров - М.: Наука, 2016. - 325 с.

    12. Булавский В.А. Численные методы линейного программирования - М.: Наука, 2017. - 367с.

    13. Болтянский В.Г. Математические методы оптимального управления - М.: Наука, 1969. - 408 с.

    14. Васильев Ф.П. Линейное программирование / Ф.П. Васильев, А.Ю. Иваницкий - М.: «Факториал», 2018. - 176 с.

    15. Гилл Ф. Практическая оптимизация / Ф. Гилл - М.: Мир, 1985. - 510с.

    16. Грот О. Оптимальные статистические решения / О. Грот - М.: Мир, 2014. - 496с.

    17. Демьянов В.Ф. Недифференцируемая оптимизация / В.Ф. Демьянов, Л.В. Васильев - М.: Наука, 2011. - 384 с.

    18. Зельдович Я.Б. Элементы прикладной математики / Я.Б. Зельдович - М.: Наука, 2012. - 592с.

    19. Кирин Н.Е. Методы последовательных оценок в задачах оптимизации управления системами / Н.Е. Кирин - Л: ЛГУ, 2010. - 160 с.

    20. Кузнецов А.В. Математическое программирование / А.В. Кузнецов, В.А. Сакович, Н.И. Холод - Минск: Высшая школа. 1994. - 285 с.

    21. Пшеничный Б.Н. Метод линеаризации / Б.Н. Пшеничный - М.: Наука, 1983. – 319 с.

    22. Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах /  Б.Н. Пшеничный, Ю.М. Данилин - М.: «Наука», 1975. - 320 с.

    23. Прикладная математика и информатика: Курс лекций / Под ред. А. А. Колесникова. Л.: ВАС, 2017. - 209 с.

    24. Реклейтис Г. Оптимизация в технике: В 2-х книгах. Пер. с англ. / Г. Реклейтис, А. Рейвиндран, К. Рэгсдел - М.: Мир, 1986.

    25. Васильев Ф.П. Численные методы решения экстремальных задач / Ф.П. Васильев - М.: Наука, 2017. – 318 с.

    26. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров - М.: Наука, 2016. – 275 с.