Например, если из 10 000 микросхем для проверки качества отобрано 200 штук, то объем генеральной совокупности равен 10 000, а выборочной – 200

Теоретическая статистика доказывает научность и правильность самой статистики.

Теоретическая математическая статистика - наука, изучающая методы раскрытия закономерностей, свойственных большим совокупностям однородных объектов, на основании их выборочного обследования. Этим разделом статистики занимаются математики, и они любят с помощь своих теоретических математических доказательств убеждать нас в том, что статистика сама по себе научна и ей можно доверять. Беда в том, что эти доказательства способны понять только другие математики, а обычным людям, которым нужно пользоваться математической статистикой эти доказательства всё равно не доступны, да и совершенно не нужны!

Вывод: Если вы не математик, то не тратьте зря свои силы на понимание теоретических выкладок по поводу математической статистики. Изучайте собственно статистические методы, а не их математические обоснования.

Прикладная статистика учит пользователей работать с любыми данными и получать обобщённые результаты. Неважно, какие именно это данные, важно, какое количество этих данных находится в вашем распоряжении. Кроме того, прикладная статистика подскажет нам, насколько можно верить в то, что полученные результаты отражают действительное положение дел.

Для разных дисциплин в прикладной статистике используют различные наборы конкретных методов. Поэтому различают следующие разделы прикладной статистики: биологическая, психологическая, экономическая и другие. Они отличаются друг от друга комплектацией примеров и приемов, а также излюбленными методами вычислений.

Можно привести следующий пример различий между применением прикладной статистики для разных дисциплин. Так, статистическое изучение режима турбулентных водных потоков производится на основе теории стационарных случайных процессов. Однако применение той же теории к анализу экономических временных рядов может привести к грубым ошибкам ввиду того, что допущение того, что распределение вероятностей сохраняется неизменным в этом случае, как правило, совершенно неприемлемо. Следовательно, для этих разных дисциплин потребуются разные статистические методы.

 

Задачи математической статистики

• Описание явлений, то есть, упорядочение поступившего статистического материала, представление его в наиболее удобном для обозрения и анализа виде (таблицы, графики).
• Анализ и прогноз, то есть приближённая оценка характеристик на основании статистических данных. Например, приближённая оценка математического ожидания и дисперсии наблюдаемой случайной величины и определение погрешностей этих оценок.
• Выработка оптимальных решений. Например, определение числа опытов n, достаточного для того, чтобы ошибка от замены теоретических числовых характеристик их экспериментальными оценками не превышала заданного значения. В связи с этим возникает задача проверки правдоподобия гипотез о параметрах распределения и о законах распределения случайной величины, решением которой является возможность сделать один из выводов:

– отбросить гипотезу, как противоречащую опытным данным;

– принять гипотезу, считать ее приемлемой.

Математическая статистика помогает экспериментатору лучше разобраться в опытных данных, полученных в результате наблюдений над случайными явлениями; оценить, значимы или не значимы наблюдаемые факты; принять или отбросить те или иные гипотезы о природе случайных явлений.

 

Основные понятия математической статистики

Генеральная совокупность – это совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины. Генеральная совокупность может быть конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность составляющих ее объектов.

Все те положения математической статистики, которые мы будем изучать, справедливы лишь для случайной выборки. Случайной выборкой (выборочной)называется такая выборка, при построении которой обеспечена одинаковая вероятность попадания в неё любого объекта генеральной совокупности. Классический способ построения случайной выборки состоит в использовании датчика равномерно распределенных случайных чисел применительно к т.н. основе выборки, т.е. к перечню всех элементов генеральной совокупности. Используются также другие способы моделирования случайности, например, механическая выборка. К числу случайных иногда относят также стратифицированную (районированную) и гнездовую (кластерную) выборки.

Например, если из 10 000 микросхем для проверки качества отобрано 200 штук, то объем генеральной совокупности равен 10 000, а выборочной – 200.

4. Статистическое распределение выборки.
Полигон и гистограмма

Статистическая совокупность, расположенная в порядке возрастания или убывания значений изучаемого признака, называется вариационным рядом, а ее объекты – вариантами. Вариационный ряд называется дискретным, если его члены принимают конкретные изолированные значения. Если элементы вариационного ряда заполняют некоторый интервал, то такой ряд называется непрерывным. Если рассматривать учебную группу студентов, то вес величина непрерывная (может быть любой в некотором диапазоне), а год рождения – величина дискретная (так же в некотором диапазоне). Практически построение решает задачу описания экспериментального материала. Однако при больших построение слишком трудоемко и не всегда наглядно по сравнению с другими видами закона распределения, например. Для придания выборочной совокупности или вариационному ряду компактности и наглядности статистический материал подвергается дополнительной обработке, т. е. строится так называемое статистическое распределение выборки.

Практически сложно получить полную информацию о случайной величине. Поэтому случайным образом отбирают объекты, которые называется выборкой, при этом число – n называется объемом выборки. Выборку делают либо из ранее полученных результатов, либо планируют эксперимент. По результатам выборки строят простой статистический ряд в виде таблицы, состоящей из двух строк, в первой – порядковый номер измерения, во второй – его результат x_i. Затем производят группировку данных. Вначале x_i располагают в порядке возрастания, интервал наблюдаемых значений случайной величины разбивают на последовательные непересекающиеся частичные интервалы, далее подсчитывают количество значений x_i, попавших в каждый интервал, т.е. n_i. Таким образом, получается группированный статистический ряд или статистическое распределение выборки. Статистическим распределением выборки или статистическим рядом называют перечень вариант и соответствующих им частот или относительных частот.

Пример 1. После группировки данных в выборке статистический ряд задан таблицей 6.1 (где объем выборки n = 15).

Таблица 6.1

i	1	2	3	4
xi	2	3	5	10
ni	5	5	3	2

 

В таблице 6.1 значения x_i называют вариантами. Последовательность вариант, записанных в возрастающем порядке (вся строка x_i) называется вариационным рядом. Число наблюдений n_i называют частотами, i – номер варианты.

Учитывая, что – это объем выборки, можно найти относительную частоту p_i=n_i/n, наблюдаемого значения x_i – варианты, k – количество вариант.

Тогда таблица 6.1 будет иметь вид:

Таблица 6.2

i	1	2	3	4
xi	2	3	5	10
ni/n	0,33	0,33	0,2	0,14

 

Табличные данные могут быть представлены графически в виде полигона или гистограммы. Если выборка задана в виде отдельных точек, а не интервалов, тогда строят полигон частот. Полигоном частот называется ломанная, отрезки которой соединяют точки (x_;; n_i/n). На рис.6.1 изображен полигон относительных частот, приведённых в таблице 6.2.

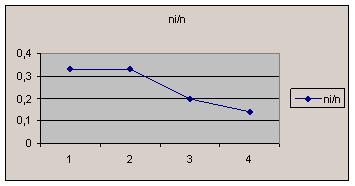
Рис. 6.1. Полигон

Пример 2. В этом примере наблюдаемые значения случайной величины после группировки данных в выборке разбиты на последовательные непересекающиеся частичные интервалы. В результате получается статистический ряд, который задан таблицей 6.3.

Таблица 6.3

i	i	1	2	3	4
xi	xi	0-2	2-4	4-6	6-8
ni/n	ni	5	10	12	3

 

Данную таблицу можно представить через относительную частоту p_i =n_i/n (где объем выборки n = 30).

Таблица 6.4

i	1	2	3	4
xi	0-2	2-4	4-6	6-8
рi=ni/n	0,17	0,33	0,4	0,1

При этом частоты р_i удовлетворяют условию 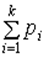=1. Если выборка задана в виде интервалов, тогда строят гистограмму. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы x_i, их высоты равны р_i =n_i/n (плотности относительной частоты). На рис. 6.2 изображена гистограмма относительных частот, приведённых в таблице 6.4.

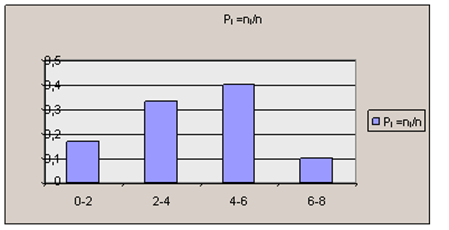
Рис. 6.2. Гистограмма