ТЕМА «ФУНКЦИИ, СВОЙСТВА И ГРАФИКИ»
СОДЕРЖАНИЕ
Пояснительная записка
1. Понятие функции. Область определения и область значений функции
2. Способы задания функции
3. Свойства функции
3.1. Четность
3.2. Периодичность
3.3. Нули функции
3.4. Монотонность
3.5. Знакопостоянство
4. Контрольные вопросы и задания
Заключение
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая тетрадь составлена в соответствии с Государственным образовательным стандартом дисциплины. Тетрадь посвящена одной из центральных тем курса алгебры и начал анализа «Функции, свойства, графики», в ней вводятся и закрепляются важнейшие теоретические понятия, без которых невозможно дальнейшее изучение этого курса.
Использование рабочей тетради значительно облегчит работу преподавателей, позволит выполнять больший объем работы на каждом занятии, повысит качество знаний и результат обучения. Задания составлены по темам в виде практических занятий. Рабочая тетрадь предназначена для обучения на всех специальностях начального, среднего и высшего профессионального образования.
ПОНЯТИЕ ФУНКЦИИ
þ Функцией называется зависимость одной переменной от другой, где каждому значению независимой переменной (х) соответствует только одно значение зависимой (у).
| Х |
| У |
| f |
| х1 |
| х2 |
| х3 |
| у1 |
| у2 |
Обозначение функции: у = f(х), где х – аргумент, у – значение функции.
þ Множество всех значений независимой переменной (Х) называется областью определения функции; обозначается D(у).
þ Множество значений зависимой переменной (У) называется областью значений функции; обозначается Е(у).
Пример 1. у = х + 2
D(у): хÎ (-∞; +∞), т.е. х – любое число.
Е(у): уÎ (-∞; +∞).
Пример 2. у = 
D(у): х≠0, т.е. хÎ(-∞; 0)È(0; +∞).
Е(у): у≠0, т.е. уÎ(-∞; 0)È(0; +∞).
Пример 3. у = 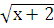
D(у): х+2 ≥ 0, х ≥ -2, т.е. хÎ [-2; +∞).
Е(у): уÎ [0; +∞).
! Задания для самостоятельной работы.
1. Найдите область определения функции у = 8 - 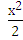
2. Найдите область значений функции у = -х2 + 5х
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
а) описанием (словесный способ).
Утром температура воздуха была +4о, днем похолодало до +2о, а вечером опустилась до -2о. Этот пример показывает зависимость между временем суток и температурой воздуха.
б) табличный.
| х | Утро | День | Вечер |
| у | +4о | +2 о | -2 о |
в) графический.
þ Графиком функции называется множество всех точек координатной плоскости с координатами (x; y), такими, что абсцисса x принимает все значения из области определения, а ордината y равна значению функции в точке x.

г) формулой (аналитический).
Пример 1. у = 3х + 1
Пример 2. у = 2х2- 2
! Задания для самостоятельной работы.
1. Дана функция. Заполните таблицу:
а) у = 3х + 1
| х | 1 | 0 | ||
| у | -2 | 5 |
б) у = 2х2- 2
| х | 0 | 1 | 10 | |
| у | 2 |
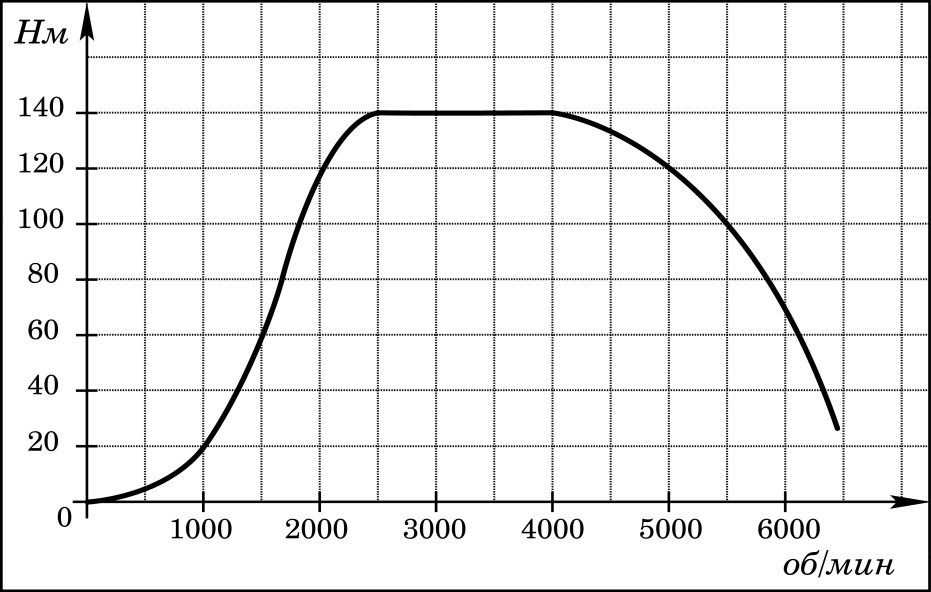
2. На графике изображена зависимость крутящего момента двигателя от числа оборотов. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться водитель, чтобы крутящий момент был не меньше 120 Нм? Ответ дайте в километрах в час.
СВОЙСТВА ФУНКЦИИ
ЧЕТНОСТЬ
þ Функция f (x) называется четной, если для любого x из ее области определения -x также принадлежит области определения, причем
f (-x) = f (x).
Свойство: график четной функции симметричен относительно оси ОУ.
Пример. у = х2
| У |
| Х |
| 0 |
þ Функция f (x) называется нечетной, если для любого x из ее области определения -x также принадлежит области определения, причем
f (-x) = - f (x).
| У |
| Х |
| 0 |
Пример. у = х3
! Задания для самостоятельной работы.
1. Что можно сказать о функции:
1) у = х4 – х2 +1;
2) у = х – 2sinх;
3) у = 3 cos х + х
а) четная; б) нечетная; в) ни четная, ни нечетная?
2. Приведите пример четной функции, нечетной функции
Периодичность
þ Функция f (x) называется периодической с периодом T ≠ 0, если для любого x, принадлежащего области определения функции, x - T, x + T также принадлежат области определения и ее значения в точках x, x - T, x + T равны, т.е. выполняется равенство f(x) = f(x-Т)= f(x+Т).
Пример. 1) у = sinх – периодическая с периодом Т = 2p,
2) у = tg x - периодическая с периодом Т = p,
3) у = х – 2 - непериодическая.
! Задания для самостоятельной работы
1. Что можно сказать о функции
а) периодическая; б) непериодическая?
1) у = 3cos(x+ p) 2) у = х – 2sin х
2. Приведите пример непериодической функции:
_____________________________________________________
Нули функции
В этом пункте рассматривается нахождение точек пересечения графика с осями координат.
1.Условие нахождения точек пересечения с осью ОХ: у = 0.
2. Условие нахождения точки пересечения с осью ОУ: х = 0.
Пример. у = 2х + 4.
у = 0, 2х + 4 = 0, х = -2.
(-2; 0) – точка пересечения с осью ОХ.
х = 0, у = 2×0 + 4 = 4.
(0; 4) – точка пересечения с осью ОУ.
! Задания для самостоятельной работы.
1.Найдите нули функции
1) у = - х2 + 5х – 9;
2) у = 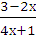 ;
;
3) у = 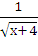 ;
;
МОНОТОННОСТЬ
þ Функция f (x)называется монотонно возрастающей на некотором интервале, если для любых значений x 1 и x 2, принадлежащих этому интервалу, таких что x 2 > x 1, выполнено неравенство f (x 2) > f (x 1).
| У |
| Х |
| 0 |
þ Функция f (x)называется монотонно убывающей на некотором интервале, если для любых значений x 1 и x 2, принадлежащих этому интервалу, таких что x 2 > x 1, выполнено неравенство f (x 2) < f (x 1).
| У |
| Х |
| 0 |
! Задания для самостоятельной работы.
1) Найдите по графику промежутки возрастания и убывания
| У |
| Х |
| 0 |
| 2 |
| 3 |
| 4 |
| -1 |
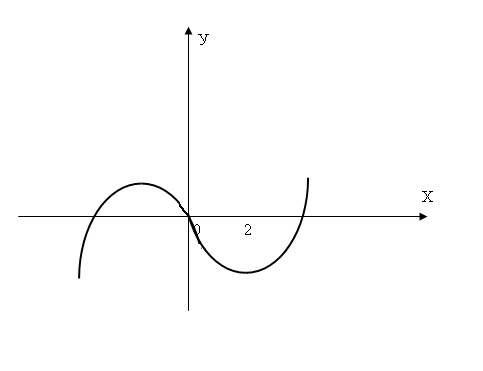
б)
2.Приведите пример возрастающей функции, убывающей функции.
 2020-07-12
2020-07-12 78
78







