2020-07-12
157
Знакопостоянством функции является условие выполнения неравенств f(x) > 0, f(x) < 0.
Если график функции расположен выше оси ОХ, то функция f(x) > 0.
Если график функции расположен ниже оси ОХ, то функция f(x) < 0.
Пример1.
| У |
| Х |
| 0 |
| 2 |
| 3 |
| 4 |
| -1 |
f(x) > 0 на (-∞; 2) È (4; +∞); f(x) < 0 на (2; 4)
Пример 2. Решить неравенство х2 – 4 > 0.
| У |
| Х |
| 0 |
| 2 |
| -2 |
| -4 |
Рассмотрим функцию у = х2 – 4
f(x) > 0 на (-∞; -2)È(2; +∞).
Ответ: х Î (-∞; -2)È(2; +∞).
б) решим методом интервалов:
(х - 2)(х + 2) > 0
| х |
| + |
| — |
| + |
| 2 |
| -2 |
| -2 |
| 2 |
Ответ: хÎ(-∞; -2) È (2; +∞),
! Задания для самостоятельной работы.
1. При каких значениях х функция f(x) < 0, если
а) у = 3 + 2х;
б) у = - 4х2 + 1;
в) у =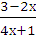 
2. Приведите пример функции, которая положительна на R, отрицательна на R.
! При описании функции y = f (x) принято указывать:
1. Область определения D(y) и область значений E(y) функции.
2. Является ли функция периодической.
3. Является ли функция четной или нечетной.
4. Точки пересечения графика с осями координат.
5. Промежутки знакопостоянства функции.
6. Интервалы возрастания и убывания.
! КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Найдите область определения функции у =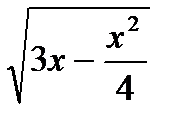 
а) (-∞; 12]; б) [-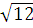 
; ];
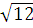в) [0; 12] г) [-12; 0].
2. Найдите область значений функции у = х2+3х-1.
а) (-∞; 1,25]; б) [-1,5; +∞);
в) (-∞; -1,5]; г) [-3,25; +∞).
3. Что можно сказать о функции у =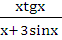 
?
а) четная; б) нечетная;
в) ни четная, ни нечетная; г) периодическая
4. Найдите «нули» функции у =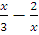 
а)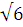 
; б) 2,45;
в) 0; 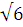; в) - ; .
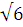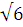5.При каких значениях x функция f(x) > 0, если f(x) =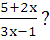 
а) (-∞; -0,4); б) (-2,5;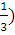 
;
в) (-0,4;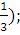 
г) (-∞; -2,5)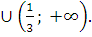 
6. Найдите промежутки возрастания функции у = 
.
а) (-∞;+∞); б) [-2; +∞);
в) (-∞; 2]; г) [-2; 2].
7. Укажите все свойства функции, график которой изображен на рисунке.
| У |
| Х |
| 0 |
| -4 |
| 4 |
| 4 |
| 2 |
| -2 |
8. Найдите координаты точки пересечения графиков функций
х + 2у = 3 и 4х + 5у = 6
а) графическим способом;
б) аналитическим (подстановкой или сложением).
