Функция распределения случайной величины, распределенной по нормальному закону

Вычислим функцию распределения случайной величины, имеющей нормальный закон распределения.

По определению функции распределения:

.

Сделаем замену переменных  и получим:

.

Первый интеграл, используя четность подынтегральной функции и то, что интеграл Эйлера – Пуассона равен , можно вычислить:

Таким образом, можно записать: .

Интеграл такого рода не выражается в элементарных функциях, но для — его нахождения используют особую функцию, так называемый интеграл вероятностей или функцию Лапласа, *" для которой составлены таблицы. Существует много разновидностей таких функций, например:

,

значения которой приведены в табл. 1 Приложений.

Именно такой вид функции Лапласа будем использовать далее.

 

 

Рис. 19. Функция Лапласа (интеграл вероятностей) Ф(t)

 

1. Ф(t) — нечетная функция, т.е. Ф(-t)=-Ф(t).

2. Ф(t) — монотонно возрастающая функция, т. е.  при ; при t>5 можно считать .

Итак, используя интеграл вероятностей или функцию Лапласа Ф(t) можно выразить функцию распределения нормального закона.

 

                                                             х

 

Рис. 20. Функция распределения нормального закона распределения

 

· Функция распределения случайной величины X, имеющей нормальный закон распределения с параметрами  и 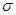, определяется по формуле:

,                                (1.43)

где  – функция Лапласа (табл. 1 Приложений).

Стандартный нормальный закон распределения

Рассмотрим очень важный частный случай нормально распределенной случайной величины.

· Нормальный закон распределения случайной величины Х с параметрами  и  (обозначается N(0;1))называется стандартным или нормированным.

· Функция плотности вероятности стандартного нормального закона:

.                             (1.44)

· Функция распределения стандартного нормального закона:

,                           (1.45)

где  – функция Лапласа (табл. 1 Приложений).

Значения функции плотности вероятности стандартного нормального закона или функции Гаусса  представлены в табл. 7 Приложений.

Функция Гаусса:

1. f(t) – четная функция, т. е. f(t)=f(-t)/

2. f(t) – монотонно убывающая функция, т. е.  при ; при t>5 можно считать .

Рис. 21. Функция Гаусса или плотности вероятности стандартного нормального закона распределения