2020-06-29
57
1. Если 
, то для нахождения вероятности попадания этой величины в заданный интервал 
используется формула:
. (1.46)
Доказательство.
Действительно, по свойству функции распределения любой непрерывной случайной величины, и, используя формулу для вычисления функции распределения случайной величины (1.43), можно записать:
,
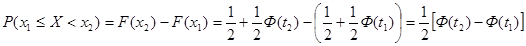где 
.
Для односторонних и симметричных интервалов, используя формулу для вычисления функции распределения нормально распределенной случайной величины (1.43), можно вывести формулы:
; (1.47)
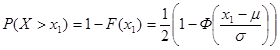. (1.48)
2. Вероятность того, что отклонение случайной величины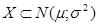 
от ее математического ожидания 
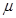не превысит величину 
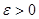(по абсолютной величине), равна:
. (1.49)
Доказательство.
Используя формулу (1.46) и свойство нечетности Лапласа, получим:
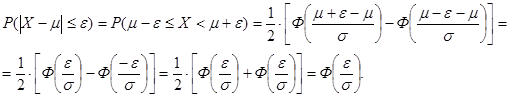
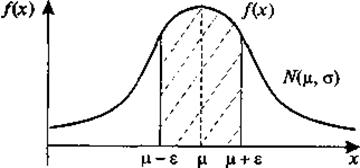
Рис. 22. Вероятность отклонения от среднего значений случайной величины Х, имеющей нормальный закон распределения
3. «Правило трех сигм».
Если случайная величина Х имеет нормальный закон распределения 
, то практически достоверно, что ее значения заключены в интервале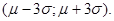 
(Вероятность «выброса» равна 0,0027).
Доказательство.
Используя формулу (1.49) и таблицу значений функции Лапласа (табл. 1 Приложений), получим:
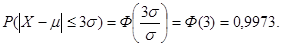
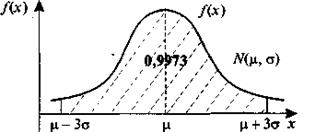
Рис. 23. «Правило трех сигм» для случайной величины Х, имеющей нормальный закон распределения
«Правило трех сигм» позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практических значений.
