Исходя из принципов построения математической модели операции, рассмотренных ранее, и общей формы ЗЛП, можно четко выделить следующие действия, необходимые для построения математической модели ЗЛП.
Во-первых, необходимо выбрать управляемые переменные, исходя из цели исследования.
Во-вторых, необходимо выразить выбранный критерий эффективности в виде целевой функции.
В-третьих, необходимо сформулировать в математическом выражении ограничения, которым должны удовлетворять переменные.
Важным при составлении функций цели и ограничений является проверка модели на соответствие единиц измерения. (Например, если коэффициенты целевой функции – cj выражаются в рублях за 1 штуку, то переменные xj должны быть выражены в штуках; если - cj – выражены в руб. за 1 тонну, то xj – тоже будет измеряться в тоннах.) Аналогично должно соблюдаться соответствие в единицах измерений между левыми и правыми частями ограничений. Нельзя допускать например, чтобы в одной части ограничения совокупность переменных выражала бы продолжительность процесса, измеряемую в часах, а в другой - переменные измерялись бы в тоннах.
Рассмотрим классическую задачу о планировании производства. Предположим, предприятие выпускает два вида продукции – А1 и А2, для производства которых используется три вида ресурсов – В1, В2, В3, запасы которых ограничены и равны соответственно – b1, b2, b3. Известны прибыль от реализации одной единицы продукции каждого вида - cj и расходные коэффициенты аij – расход i – го вида ресурса для производства одной единицы продукции j – го вида 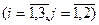 . Определить такой план выпуска продукции каждого вида, при котором суммарная прибыль от реализации всей продукции была бы максимальной. Для наглядности представим исходные данные в следующей таблице:
. Определить такой план выпуска продукции каждого вида, при котором суммарная прибыль от реализации всей продукции была бы максимальной. Для наглядности представим исходные данные в следующей таблице:
| А1 | А2 | Запас | |
| В1 | а11 | а12 | b1 |
| В2 | а21 | а22 | b2 |
| В3 | а31 | а32 | b3 |
| Прибыль за 1 ед. | с1 | с2 |
Из условия задачи можно выделить цель исследования – получение максимальной прибыли от реализации готовой продукции, достижение этой цели будет зависеть от количества произведенной продукции. Таким образом, первый вопрос, который необходимо было рассмотреть при построении математической модели, решен – в качестве управляемых переменных следует выбрать xj – количество выпускаемой продукции каждого вида.
Тогда выражение для целевой функций можно записать как сумму прибыли, получаемой от реализации каждого вида продукции, то есть:
 (3.7)
(3.7)
Следовательно, выполнен второй шаг построения математической модели – сформулирован критерий оптимальности.
На третьем шаге осталось сформулировать запись в математической форме всех необходимых ограничений. Сначала можно дать словесную формулировку возможных ограничений. Из условия задачи следует, что ограничения задачи могут быть связаны с запасами ресурсов, то есть расход каждого вида ресурса, необходимый для выпуска всей продукции, не должен превышать запаса этого ресурса. Итак, расход первого вида ресурса, необходимый для производства всей продукции, можно выразить соотношением - 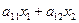 , значение которого не должно превышать запаса этого ресурса – b1. таким образом, получаем следующие ограничения:
, значение которого не должно превышать запаса этого ресурса – b1. таким образом, получаем следующие ограничения:
В1:  (3.8)
(3.8)
В2: 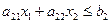 (3.9)
(3.9)
В3: 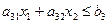 (3.10)
(3.10)
Последнее действие, завершающее построение модели, - составление дополнительных ограничений. Очевидно, что в данной задаче дополнительным ограничением будет условие неотрицательности управляемых переменных:
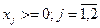 (3.11)
(3.11)
Хотя рассмотренная задача и относится к классической задаче о планировании производства, математическая модель которой выражается соотношениями (3.7 – 3.11), существует множество вариантов практических приложений задачи данного типа.
Одним из таких приложений является так называемая задача о диете или задача о составлении смесей. Используя обозначения предыдущей задачи, рассмотрим смысловое содержание задачи о диете.
Пусть А1 и А2 - компоненты, необходимые для изготовления некоторой смеси (например, для животноводческой фермы – смесь – это корм для скота), которая должна содержать три вида питательных веществ - В1, В2, В3, минимальные нормы которых в суточном рационе равны соответственно - b1, b2, b3. Известна стоимость 1 кг компонента каждого вида – cj и аij – содержание i – го питательного вещества в 1 кг компонента j - го вида. Требуется составить такой суточный рацион, который имел бы минимальную стоимость.
По аналогии с предыдущей задачей сведем исходные данные в таблицу:
| А1 | А2 | Норма | |
| В1 | а11 | а12 | b1 |
| В2 | а21 | а22 | b2 |
| В3 | а31 | а32 | b3 |
| Стоимость за 1 кг | с1 | с2 |
Построение математической модели также будет аналогичным, за исключением следующих моментов.
В качестве управляемых переменных xj следует выбрать количество компонентов (в кг) каждого вида в смеси, так как критерий эффективности – стоимость смеси – будет зависеть от весового количества компонентов. Следовательно, целевая функция будет иметь вид:

В ограничениях следует указать, что содержание питательных веществ в смеси не должно быть меньше установленной нормы, то есть:
В1: 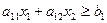
В2: 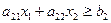
В3: 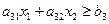
Дополнительные ограничения:  .
.
 2020-06-29
2020-06-29 607
607







