2020-06-29
93
Световые волны после щели распространяются во всех направлениях, но большая часть энергии приходится на сектор 
. При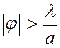 
интенсивность рассеянного излучения невелика, поэтому можно считать, что условие определяет граничное значение угла рассеивания. Значит, угол дифракции заключен в пределах
. (7)
Чем уже щель (чем меньше а), тем шире пучок света, прошедшего через эту щель (тем больше 
).
Опишем теперь эту же ситуацию, пользуясь представлением о пучке света как совокупности фотонов. Энергия и импульс фотона:
, 
.
До прохождения через щель импульс фотона 
был направлен вдоль оси z, поперечная составляющая импульса была равна нулю (
), а неопределенность по координате х равна ∞. Расширение светового пучка при прохождении света через щель означает, что у фотона появляется составляющая импульса вдоль оси х (
). При этом неопределенность по координате 
будет равна ширине щели а (рис. 4). Считая, что угол определяется первым дифракционным минимумом, имеем (угол - мал, 
):
|
|
|
.
. Следовательно,
. (8)
Мы учитывали только центральный максимум (см. рис. 2). С учетом максимумов более высоких порядков неопределенность по импульсу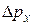 
может быть еще больше, и соотношение неопределенностей Гейзенберга нужно записать в виде:
. (9)
Смысл его состоит в том, что чем точнее определена одна из величин 
или х, тем неопределенней становится другая. Фотон не может иметь одновременно абсолютно точных значений координаты и соответствующей проекции импульса. Соотношение (6), безусловно, применимо и для электронов и для других микрочастиц. Это один из важнейших законов микромира. Для удобства оценки результатов эксперимента можно ввести параметр
(10)
Из рис. 4 следует, что 
. Поэтому 
.
Подставим найденное выражение для 
в (8). После сокращения на h получаем, что при выполнении условия (8) параметр F должен быть равен 1:
.
