Геометрический смысл производной

Систематизация знаний по теме

«Производная функции»

 

 

Вопросы консультации:

Повторение:

Физический и геометрический смыслы производной.

Формула касательной к производной.

3. - Определение производной функции;

- Теоремы о производных;

- Таблица производных элементарных функций.

Решение примеров на взятие производной функций.

 

Вопрос 1. Физический и геометрический смыслы производной

 

При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x ) получать новую функцию, которую называют производной функцией (или просто производной ) данной функции f(x)  и обозначают символом

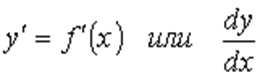
Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f'(x), называют дифференцированием и состоит он из следующих трех шагов:

1) даем аргументу x приращение D x и определяем соответствующее приращение функции

D y = f(x+D x) -f(x );

 

2) составляем отношение   ;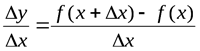

3) считая x постоянным, а D x→ 0, находим предел

,

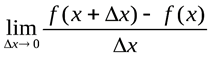который обозначаем через f (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.

Определение:

Производной y'=f' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, то есть конечен.

Таким образом, 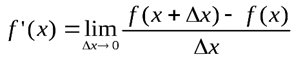, или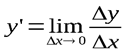

Заметим, что если при некотором значении x, например при x=a, отношение 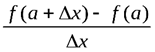  при D x→0 ¦₀  не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

Геометрический смысл производной

Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x₀

 

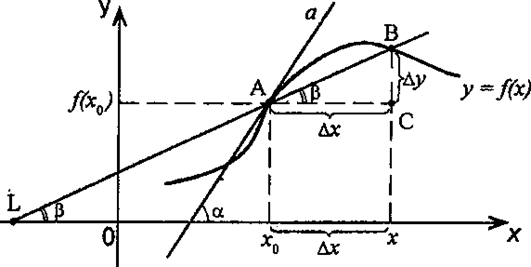
Рассмотрим произвольную прямую, проходящую через точку графика функции – точку А(x₀, f (х₀)) и пересекающую график в некоторой точке B(x;f(x)).

Такая прямая (АВ) называется секущей.

Из ∆АВС:   АС = ∆x;     ВС =∆у;     tgβ=∆y/∆x.

Так как АС || Ox, то ÐALO = ÐBAC = β (как соответственные при параллельных).

Но ÐALO – это угол наклона секущей АВ к положительному направлению оси Ох.

Значит, tgβ = k – это угловой коэффициент прямой АВ.

Теперь будем уменьшать ∆х, то есть ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться.

Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.

Если перейти к пределу при ∆х → 0 в равенстве tgβ =∆y/∆x, то получим:

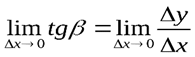или tga =f '(x₀), так как ,

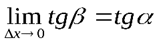где a -угол наклона касательной к положительному направлению оси Ох.

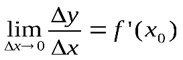 (по определению производной).

Но tga = k – это угловой коэффициент касательной, значит,

k = tga = f '(x₀).

Итак, геометрический смысл производной заключается в следующем:

Производная функции в точке x₀ равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x₀.