2020-06-29
139
Смысл каждого элемента, который входит в уравнение касательной:
1) (
– точка касания касательной и графика функции.
2) 
– угловой коэффициент касательной к графику функции.
3) 
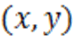– произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что 
– это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Алгоритм составления уравнения касательной
К графику функции
Задача
К кривой 
в точке с абсциссой 
провести касательную.
Рис. Касательная к графику функции 
.
Зафиксируем точку 
. Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найдем 
и точку касания:
– дано.
Точка касания: (
; 
.
2) Найдем производную в любой точке 
.
.
3) Найдем значение производной в точке с абсциссой 
.
.
4) Запишем и проанализируем уравнение касательной.
.
Упрощаем и получаем уравнение: 
.
Ответ: 
.
Касательная к графику тригонометрической функции
Дана функция 
. Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Нахождение точки касания.
1. 
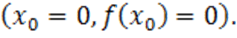Точка касания имеет координаты 
.
2. Найдем 
.
3. Найдем 
4. Запишем уравнение касательной:
.
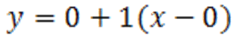5. Упростим полученное уравнение: 
.
Заметим в точке 
синусоида и касательная соприкасаются. В районе точки 
синусоида и прямая почти не различаются.
Решение задач, сопутствующих данной теме
Задача 1
Пусть дано уравнение касательной 
.
Найти точки пересечения касательной с осями координат.
Решение:
Если 
, то 
. 
– это первая точка.
Если 
, то 
. 
– вторая точка.
Итак, первая точка – это точка 
с координатами 
.
Вторая точка – точка пересечения с осью 
, точка 
с координатами 
:
Задача 2
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка 
.
Решение:
Рассмотрим прямоугольный треугольник 
(Рис. выше):
Длина катета 
равна 1.
Длина катета 
.
Длину отрезка 
из прямоугольного треугольника найдем по теореме Пифагора:
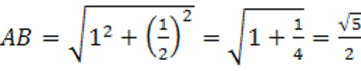
Ответ: АВ=√5/2
Задача 3
Найти площадь треугольника, образованного касательной и осями координат.
Решение:
Ясно, что это площадь треугольника 
(Рис.выше) – площадь треугольника, образованного касательной и осями координат.
Ответ: S∆АОВ=1/4
Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.
Домашнее задание по вопросу 2:
Найти радиус окружности, вписанной в треугольник 
(см. рис. к задаче 1).
Радиус окружности, описанной около треугольника 
.
Вопрос 3 (представленные формулы и теоремы - выучить):
Определение производной функции:
Производной функции y=f(x) в точке х0 называется предел отношения приращения функции в точке х0 к приращению аргумента, когда приращение аргумента стремится к нулю:
Теоремы о производных:
1. Производная суммы:
.
2. Производная от произведения:
.
