Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t).
Известно (из курса физики), что средняя скорость за промежуток времени [t0; t0+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, то есть
Vср = ∆x/∆t.
Перейдем к пределу в последнем равенстве при ∆t → 0 и получим мгновенную скорость в момент времени t0:
lim Vср (t) = n(t0).
∆t → 0
Из определения производной, предел – это отношение приращения аргумента к приращению времени (в данной физической задаче): ∆x/∆t = x'(t0).
Итак,
n(t) =x'(t).
Физический смысл производной заключается в следующем: производная функции y=f(x) в точке x0 – это скорость изменения функции f (х) в точке x0 .
Производная применяется в физике:
- для нахождения скорости по известной функции координаты от времени,
- для нахождения ускорения по известной функции скорости от времени.
u(t) = x'(t) - скорость,
a(f) = n'(t) - ускорение, или a(t) = x"(t).
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) – изменение угла от времени,
ω = φ'(t) – угловая скорость,
ε = φ'(t) – угловое ускорение, или ε = φ"(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) – масса,
x Î [0; l],l – длина стержня,
р = m'(х) – линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний.
Так, по закону Гука:
F = -kx,
где x – переменная координата,
k – коэффициент упругости пружины.
Приняв ω2=k/m, получим дифференциальное уравнение пружинного маятника:
х"(t) + ω2x(t) = 0,
где ω = √k/√m – частота колебаний (l/c),
k – жесткость пружины (H/m).
Уравнение вида у" + ω2y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных).
Решением таких уравнений является функция
у = Asin(ωt + φ0) или у = Acos(ωt + φ0),
где А – амплитуда колебаний,
ω – циклическая частота,
φ0 – начальная фаза.
Вопрос 2. Уравнение касательной
К графику функции
Нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую 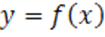 (см. рис.1).
(см. рис.1).
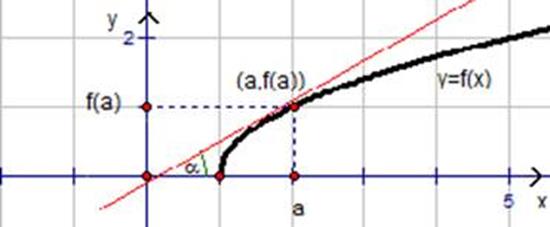
Рис. 1. График функции 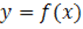 .
.
Зафиксируем точку 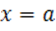 . Если
. Если 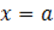 , то значение функции равно
, то значение функции равно 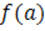 . Значит, имеем точку с координатами
. Значит, имеем точку с координатами
(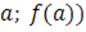 .
.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции 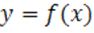 в точке с абсциссой
в точке с абсциссой 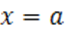 , в которой
, в которой 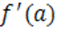 – существует.
– существует.
Уравнение касательной – это прямая, которая задается формулой 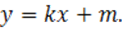
Любая прямая, в том числе и касательная, определяется двумя числами: 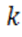 и
и 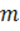 .
.
Исходя из геометрического смысла производной 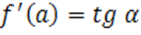 (тангенс угла наклона касательной) – это есть угловой коэффициент
(тангенс угла наклона касательной) – это есть угловой коэффициент 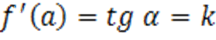 .
.
Параметр 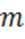 найдем из условия, что касательная проходит через точку (
найдем из условия, что касательная проходит через точку (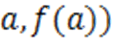 , то есть
, то есть 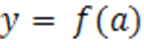 .
.
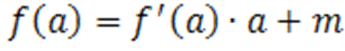 .
.
Стало быть 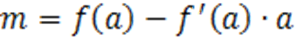 .
.
Запишем уравнение касательной
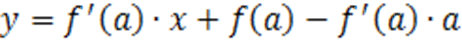 .
.
Или, 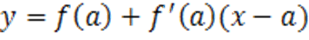 .
.
Получили уравнение касательной к кривой 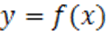 в точке с абсциссой
в точке с абсциссой 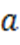 .
.
 2020-06-29
2020-06-29 129
129








