Задача 4.
Определите внутреннюю энергию аргона массой  г при температуре
г при температуре  оС.
оС.
Дано:
 г
г
 оС
оС
Найти:
 —?
—?
Решение
Думаем: для нахождения внутренней энергии воспользуемся определением внутренней энергии.
 (1)
(1)
Неизвестное химическое количество найдём из его определения:
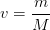 (2)
(2)
А молярная масса ( ) — табличный параметр, характеризующий данный нам в задаче газ (аргон).
) — табличный параметр, характеризующий данный нам в задаче газ (аргон).
Решаем: собственно осталось подставить (2) в (1).
 (3)
(3)
Считаем: для подсчёта используем табличный параметр молярной массы аргона ( г/моль
г/моль  кг/моль) и значение газовой постоянной (
кг/моль) и значение газовой постоянной ( м
м  *кг*с
*кг*с  *К
*К  *Моль
*Моль  ). Кроме того необходимо перевести температуру газа в кельвины: (
). Кроме того необходимо перевести температуру газа в кельвины: ( ), а массу тела перевести в килограммы (
), а массу тела перевести в килограммы ( г
г  кг).
кг).
Тогда:
 Дж
Дж
Ответ:  Дж.
Дж.
Решить задачу самостоятельно.
Задача 5.
Газ, давление которого  МПа, изобарно расширяется. При этом сила давления газа совершает работу
МПа, изобарно расширяется. При этом сила давления газа совершает работу  Дж. Определите, на сколько увеличился объём газа.
Дж. Определите, на сколько увеличился объём газа.
Дано:
 МПа
МПа
 Дж
Дж
Найти:
 —?
—?
Решение
Думаем: слово "изобарно" говорит об изопроцессе при котором постоянным является параметром давления. Неизвестное изменение объёма можно связать с работой газа:
 (1)
(1)
По сути у нас всё есть.
Решаем:
Задача 6.
Идеальный газ определённой массы при температуре 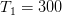 К и давлении
К и давлении  МПа занимает объём
МПа занимает объём  м3. Определите работу, совершённую силой давления газа при его изобарном нагревании до температуры
м3. Определите работу, совершённую силой давления газа при его изобарном нагревании до температуры  К.
К.
Дано:
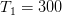 К
К
 МПа
МПа
 К
К
 м3
м3
Найти:
 —?
—?
Решение
Думаем: работу при изобарном нагревании можно найти исходя из определения:
 (1)
(1)
Вопросы об изменении объёма связаны с уравнением Менделеева-Клапейрона:
 (2)
(2)
Решаем: вопрос об изменении объёма можем проанализировать через метод банок. Нарисуем баллоны и запишем в них все параметры газа, которые необходимы для соотношения (1). Формой сосуда (изменение объёма) можно пренебречь, поэтому визуализируем сосуд с газом в первом и втором состоянии одинаковой банкой (рис. 1).

Рис. 1. Параметры системы
Банка 1 — начальное состояние системы. Газ находится при начальном давлении ( ), начальной температуре (
), начальной температуре ( ) и начальном объёме (
) и начальном объёме (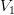 ). При этом химическое количество вещества (
). При этом химическое количество вещества ( ), которое в описанных в задаче процессах не изменяется.
), которое в описанных в задаче процессах не изменяется.
Реализуем (2) в этом случае:
 (3)
(3)
Банка 2 — следующее состояние системы. Объём газа при этом  , давление при условии изобарности, заданной в задаче —
, давление при условии изобарности, заданной в задаче —  , температура новая —
, температура новая —  и изначальное химическое количество (
и изначальное химическое количество ( ). Реализуем (2) в этом случае:
). Реализуем (2) в этом случае:
 (4)
(4)
Работа газа, описанная в (1) может быть записана в виде:
 (5)
(5)
Если произведение  у нас уже дано, но с
у нас уже дано, но с  ещё нужно повозиться. Для этого поделим (4) на (3):
ещё нужно повозиться. Для этого поделим (4) на (3):
 (6)
(6)
Выразим из (6)  :
:
 (7)
(7)
Осталось подставить (7) в (5):
 (8)
(8)
Считаем:
 Дж
Дж
Ответ:  Дж.
Дж.
 2020-06-29
2020-06-29 125
125








