К практическому занятию №3

Задание № 1

Фирма набирает штат сотрудников и располагает четырьмя группами различных должностей, причем в каждой группе 5, 3, 6, 4 вакансий, соответственно. Кандидаты на должность проходят тестирование, по результатам которого их разделяют на 3 группы – по 7, 5, 6 человек в каждой группе. Для каждого кандидата отобранных в i -ю группу требуются определенные затраты 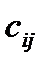  у.е. на обучение для занятия должности в j -й группе, представленные следующей матрицей

 .

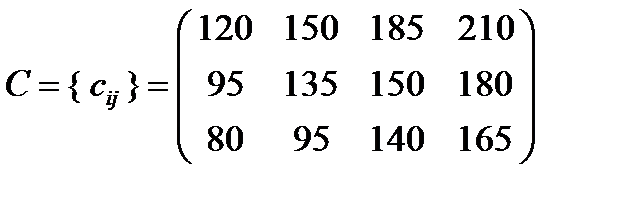Необходимо распределить кандидатов на должности, затратив минимальные средства на их обучение.

Задание № 2

 

Фермер располагает тремя участками земли I, II, III, имеющими площади 580 га, 230 га и 360 га, соответственно. Он планирует засеять пшеницей 180 га, рожью – 350 га, просом – 290 га, кукурузой – 110 га и ячменем -240 га. Предполагаемые урожайности (в центнерах) культур с одного гектара каждого участка земли приведены в таблице:

 

Район расположения участков земли	Урожайность культур (центнеров с гектара)
	Пшеница	Рожь	Просо	Кукуруза	Ячмень
I	24	15	21	32	20
II	12	6	17	9	14
III	18	20	13	9	15

 

Найдите оптимальный план засева участков сельскохозяйственными культурами, при котором суммарный урожай оказывается наибольшим.

 

Задание № 3

 

Инвестор, намереваясь приступить к постройке шести объектов с номерами 1, 2, …, 6, рассматривает предложения шести строительных компаний A, B, …, F, каждую из которых он оценивает неким комплексным показателем, значения которого приведены в таблице (наилучшее значение показателя соответствует его минимуму):

 

№ объектов	1	2	3	4	5	6
Компании
A	2	2	12	1	3	5
B	6	9	5	3	6	7
C	4	2	7	4	2	3
D	1	3	2	5	5	1
E	4	4	5	6	8	4
F	8	8	4	2	9	2

 

Инвестору необходимо поручить строительство объектов строительным компаниям, исходя из условия минимизации суммарного показателя, учитывая при этом, что один объект может возводиться только одной строительной компанией и одна компания может возводить только один объект.