Контрольная работа №8
По математической статистике
Задача 1
В результате проведения исследований получены следующие статистические данные (табл.1), где  – частота попадания вариант в промежуток
– частота попадания вариант в промежуток  . Для выборки построить гистограмму относительных частот.
. Для выборки построить гистограмму относительных частот.
Задача 2
Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты) и найти несмещенные оценки генерального среднего и генеральной дисперсии на основании данного распределения выборки (табл.2).
Задача 3
Найти доверительный интервал для неизвестного математического ожидания а случайной величины Х, распределенной нормально, если известны объем выборки n, выборочное среднее  , надежность
, надежность  и среднее квадратическое отклонение
и среднее квадратическое отклонение 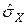 (табл.3).
(табл.3).
Задача 4
Генеральная совокупность имеет нормальное распределение, для которого известно значение параметра  . Найти наименьший объем выборки, при котором доверительный интервал длиной
. Найти наименьший объем выборки, при котором доверительный интервал длиной  покрывает параметр а с надежностью
покрывает параметр а с надежностью  (табл.4).
(табл.4).
Задача 5
Найти доверительный интервал для неизвестного среднего квадратического отклонения  нормально распределенной случайной величины Х, если известны объем выборки n, надежность
нормально распределенной случайной величины Х, если известны объем выборки n, надежность  и выборочная дисперсия
и выборочная дисперсия  (табл.5).
(табл.5).
ОБРАЗЕЦ РЕШЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Задача 1
В результате проведения исследований получены следующие статистические данные (табл.1), где  – частота попадания вариант в промежуток (
– частота попадания вариант в промежуток ( ]. Для выборки построить гистограмму относительных частот.
]. Для выборки построить гистограмму относительных частот.
| i | 
| 
|
| 1 2 3 4 5 | 1 – 3 3 – 5 5 – 7 7 – 9 9 – 11 | 18 10 12 11 9 |
Решение.
Объём выборки n =50. Найдём относительные частоты:
w 1=4/50=0,08, w 2=10/50=0,2, w 3=12/50=0,24, w 4=11/50=0,22, w 5=9/50=0,18.
Найдём плотности относительных частот, учитывая, что длина интервала h =2:
w 1/ h =0,08/2=0,04, w 2/ h =0,2/2=0,1, w 3/ h =0,24/2=0,12, w 4/ h =0,22/2=0,11, w 5/ h =0,18/2=0,9.
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от неё на расстояниях, равных соответствующим плотностям относительной частоты.
Например, над интервалом (1,3) проведем отрезок, параллельный оси абсцисс и находящийся от неё на расстоянии, равном 0,04; аналогично строят остальные отрезки. Искомая гистограмма относительных частот изображена на рисунке ниже.

Задача 2
В ходе эксперимента получены данные наблюдений:

| 14 | 15 | 16 | 17 | 18 | 19 | 20 |

| 6 | 10 | 18 | 28 | 20 | 12 | 6 |
Для данной выборки выполнить следующее:
· Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты);
· Найти несмещенные оценки генерального среднего и генеральной дисперсии.
Решение.
Найдем числовые характеристики данной выборки:
1. Минимальное и максимальное значение выборки:  .
.
2. Размах выборки: 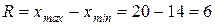 .
.
3. Мода:  .
.
4. Так как вариационный ряд содержит четное число вариант (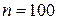 ), то медиана
), то медиана  .
.
5. Выборочное среднее:  .
.
6. Выборочная дисперсия: 
 .
.
7. Среднее квадратическое отклонение:  .
.
8. Начальные моменты:  ,
,  ,
,

9. Центральные моменты:  ,
,  ,
,  ,
,
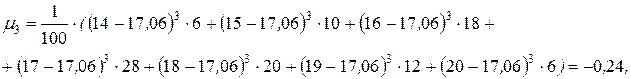

Несмещенной оценкой генерального среднего является выборочное среднее.  .
.
Для вычисления выборочной дисперсии воспользуемся формулой:
 .
.
 ,
,  .
.
Находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию):  .
.
Задача 3
Найти доверительный интервал для неизвестного математического ожидания а случайной величины Х, распределенной нормально, если известны объем выборки n =30, выборочное среднее  , надежность
, надежность  и среднее квадратическое отклонение
и среднее квадратическое отклонение  .
.
Решение.
Построим доверительный интервал для математического ожидания при неизвестном параметре  . Воспользуемся формулой (30):
. Воспользуемся формулой (30):
 .
.
Для заданных  и
и 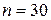 найдем значение
найдем значение  (см. Приложение 6). Тогда получим интервал, покрывающий
(см. Приложение 6). Тогда получим интервал, покрывающий  с надежностью 0,99:
с надежностью 0,99:
 .
.
Задача 4
Генеральная совокупность имеет нормальное распределение, для которого известно значение параметра  . Найти наименьший объем выборки, при котором доверительный интервал длиной
. Найти наименьший объем выборки, при котором доверительный интервал длиной  покрывает параметр а с надежностью
покрывает параметр а с надежностью  =0,95.
=0,95.
Решение.
Доверительный интервал для математического ожидания при известном параметре  определяется формулой (25):
определяется формулой (25):  или
или 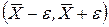 , где
, где  . По условию
. По условию  , значит,
, значит,  . Величину
. Величину  найдем из уравнения
найдем из уравнения  (см. Приложение 2). Тогда
(см. Приложение 2). Тогда  .
.
Следовательно, наименьшим объемом выборки будет  .
.
Задача 5
Найти доверительный интервал для неизвестного среднего квадратического отклонения  нормально распределенной случайной величины Х, если известны объем выборки n =20, надежность
нормально распределенной случайной величины Х, если известны объем выборки n =20, надежность  и выборочная дисперсия
и выборочная дисперсия  .
.
Решение.
Доверительный интервал для неизвестного среднего квадратического отклонения  определяется формулой (37):
определяется формулой (37): 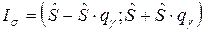 .
.
Вычислим  , тогда
, тогда 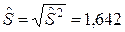 . Найдем величину
. Найдем величину  по известному
по известному  (см. Приложение 7):
(см. Приложение 7):  . Следовательно, интервал
. Следовательно, интервал  является доверительным для параметра
является доверительным для параметра  с надежностью
с надежностью  .
.
ПОЯСНЕНИЕ
Номер варианта в контрольной работе №8 совпадает с последней цифрой номера зачетной книжки.
Таблица 1. Варианты задачи 1.
| Вариант | i | 
| 
|
| Вариант | i | 
| 
|
| 1 | 1 2 3 4 5 | 3 – 7 7 – 11 11 – 15 15 – 19 19 – 23 | 4 6 9 10 11 | 6 | 1 2 3 4 5 | 4 – 6 6 – 8 8 – 10 10 – 12 12 – 14 | 3 9 7 22 9 | |
| 2 | 1 2 3 4 5 | 4 – 8 8 – 12 12 – 16 16 – 20 20 – 24 | 5 7 10 12 6 | 7 | 1 2 3 4 5 | 1 – 5 5 – 9 9 – 13 13 – 17 17 – 21 | 4 5 9 10 2 | |
| 3 | 1 2 3 4 5 | 2 – 4 4 – 6 6 – 8 8 – 10 10 – 12 | 5 8 16 12 9 | 8 | 1 2 3 4 5 | 5 – 7 7 – 9 9 – 11 11 – 13 13 – 15 | 4 14 12 8 2 | |
| 4 | 1 2 3 4 5 | 7 – 9 9 – 11 11 – 13 13 – 15 15 – 17 | 5 4 8 12 11 | 9 | 1 2 3 4 5 | 2 – 5 5 – 8 8 – 11 11 – 14 14 – 17 | 5 24 13 1 6 | |
| 5 | 1 2 3 4 5 | 5 – 8 8 – 11 11 – 14 14 – 17 17 –20 | 5 7 4 1 3 | 0 | 1 2 3 4 5 | 3 – 7 7 – 11 11 – 15 15 – 19 19 – 23 | 6 8 10 12 4 |
 2020-06-30
2020-06-30 243
243







